《最优化理论》作业1.1：梯度下降法

Zephus · 发表于 2021-12-18 11:15

多元实函数的一阶泰勒展开式

不妨设函数  是定义在空间 $D$ 的多元实函数，若  在点 $\overset{\frown}{\mathbf{x}} \in D$ 领域内连续且存在偏导数，那么由泰勒近似定理得一阶泰勒展开式：

$f(\mathbf{x}) \approx p_1(\mathbf{x}) = f(\overset{\frown}{\mathbf{x}}) + [\nabla f(\overset{\frown}{\mathbf{x}})]^\mathrm{T}(\mathbf{x} -\overset{\frown}{\mathbf{x}}) \tag{1}$
可以证明，  和  在  有相同的零阶导和一阶导，但  的高阶导均为零。可以说，  提取了  在  处一阶导及以下的所有信息。
梯度下降法

改写公式(1)得：

$f(\mathbf{x}) - f(\overset{\frown}{\mathbf{x}}) = [\nabla f(\overset{\frown}{\mathbf{x}})]^\mathrm{T}(\mathbf{x} -\overset{\frown}{\mathbf{x}}) \tag{2}$
梯度下降法得的化指标是让 $f(\mathbf{x})$ 最小，也就是让公式(2)的左边最小。将公式(2)的右边展开得：

$\begin{aligned} \left[\nabla f(\overset{\frown}{\mathbf{x}})\right]^\mathrm{T}(\mathbf{x} - \overset{\frown}{\mathbf{x}}) &\Leftrightarrow <(f_{x_1}, f_{x_2}, \dots, f_{x_N}), (x_1 - \overset{\frown}{x_1}, x_2 - \overset{\frown}{x_2}, \dots, x_N - \overset{\frown}{x_N})> \\ &= \Vert\nabla f(\overset{\frown}{\mathbf{x}})\Vert_2\Vert\mathbf{x} - \overset{\frown}{\mathbf{x}}\Vert_2\cos(\theta) \end{aligned}\tag{3}$
当 $\theta = \pi$ ，即 $\mathbf{x} - \overset{\frown}{\mathbf{x}} = -\lambda\nabla f(\overset{\frown}{\mathbf{x}}), \lambda > 0$ ，公式(3)取得最小值，因此梯度下降的更新公式为：

$\mathbf{x} = \overset{\frown}{\mathbf{x}} - \lambda\nabla f(\overset{\frown}{\mathbf{x}}), \lambda > 0 \tag{4}$
基于中心差分求梯度的数值解

要求 $\nabla f(\overset{\frown}{\mathbf{x}})$ ，只需求各元的偏导数。对于显示表达式的  ，很容易求出偏导数的解析解。若未知表达式，可以根据偏微分的定义求偏导数的数值解。

$\mathrm{d}y = f(\overset{\frown}{\mathbf{x}}) - f(\overset{\frown}{\mathbf{x}} - \mathrm{d}\overset{\frown}{\mathbf{x}}) = \sum_i f_{\overset{\frown}{x}_i}\mathrm{d}\overset{\frown}{x}_i + o(\Vert\mathrm{d}\overset{\frown}{\mathbf{x}}\Vert_2) \tag{5}$
只需令 $\mathrm{d}x_i \neq 0$ ,其他均为零，那么可以求出 $f_{x_i}$ 。由微分中值定理得，采用中心微分求偏导数的数值解。

$f_{\overset{\frown}{x}_i} = \frac{f(\overset{\frown}{\mathbf{x}} + (0, \dots, \mathrm{d}\overset{\frown}{x}_i, \dots, 0)^\mathrm{T}) -f(\overset{\frown}{\mathbf{x}} - (0, \dots, \mathrm{d}\overset{\frown}{x}_i, \dots, 0)^\mathrm{T}) }{2\mathrm{d}\overset{\frown}{x}_i} \tag{6}$
常令 $\mathrm{d}\overset{\frown}{x}_i = 10^{-7}$ 。
最终代码

#! -*- coding:utf-8 -*-

#! -*- coding:utf-8 -*-

&#39;&#39;&#39;
@Author:       ZM
@Date and Time: 2021/11/7 9:08
@File:       GD.py
&#39;&#39;&#39;

import numpy as np
import matplotlib.pyplot as plt

&#39;&#39;&#39;待优化的实函数 f(x) = x0 * x0 / 4 + x1 * x1，很多情况不知函数表达式
&#39;&#39;&#39;
def fun(x: np.ndarray):
return x[0] * x[0] / 4 + x[1] * x[1]

&#39;&#39;&#39;基于中心差分求梯度
&#39;&#39;&#39;
class GradFun:
def __init__(self, f):
      self.f = f

def __call__(self, x: np.ndarray):
      h = 1e-14
      grad = np.zeros_like(x, dtype=x.dtype)

      for idx in range(x.size):
         tmp_val = x[idx]
         x[idx] = tmp_val + h
         fxh1 = self.f(x)

         x[idx] = tmp_val - h
         fxh2 = self.f(x)

         grad[idx] = (fxh1 - fxh2) / (2 * h)
         x[idx] = tmp_val

      return grad

&#39;&#39;&#39;可视化
&#39;&#39;&#39;

def plot_fun(f):
&#39;&#39;&#39;绘制函数f的曲面图
&#39;&#39;&#39;
fig = plt.figure()
ax = plt.axes(projection=&#39;3d&#39;)
x1 = np.linspace(-1, 1, num=50)
x2 = np.linspace(-1, 1, num=50)
X1, X2 = np.meshgrid(x1, x2)
FX = f(np.concatenate([X1[None, ...], X2[None, ...]], axis=0))
ax.plot_surface(X1, X2, FX, rstride=1, cstride=1, cmap=&#39;viridis&#39;, edgecolor=&#39;none&#39;)
fig.savefig(&#39;fun.png&#39;)
plt.close()

def plot_training_curve(data, best_data, name=None):
&#39;&#39;&#39;绘制梯度下降法搜索路径
&#39;&#39;&#39;
fig = plt.figure()
ax = plt.axes(projection=&#39;3d&#39;)
ax.scatter3D(*data[0])
ax.scatter3D(*best_data)
ax.plot3D(data[:, 0], data[:, 1], data[:, 2], &#39;#FA7F6F&#39;)
ax.set(title=&#39;Gradient descent&#39;)
if name is not None:
      fig.savefig(f&#39;{name}.png&#39;)
plt.close()

grad_fun = GradFun(fun)

x = np.random.randn(2)                         # 随机初始化
alpha = 1.                                     # 初始步长

min_alpha = 1e-3                               # 最小步长
cnt = 0                                        # 控制更新步长
total_steps = 600
best_fx = fun(x)
log_data = [[*x, best_fx]]                   # 用于绘制搜索曲线
best_data = [*x, best_fx]
plot_fun(fun)

&#39;&#39;&#39;梯度下降法
&#39;&#39;&#39;
for step in range(total_steps):
grad_x = grad_fun(x)
x -= alpha * grad_x

tmp_val = fun(x)
log_data.append([*x, tmp_val])
if best_fx > tmp_val:
      best_fx = tmp_val
      best_data = [*x, best_fx]
      cnt = 0
else:
      cnt += 1
      if cnt > 30: # 连续30次迭代无变化，降低步长
         alpha *= 0.1
         alpha = max(alpha, min_alpha)
         cnt = 0

log_data = np.array(log_data, dtype=&#39;float32&#39;)
print(log_data)
plot_training_curve(log_data, best_data, name=&#39;GD&#39;)效果截图

图1 待优化的函数图像

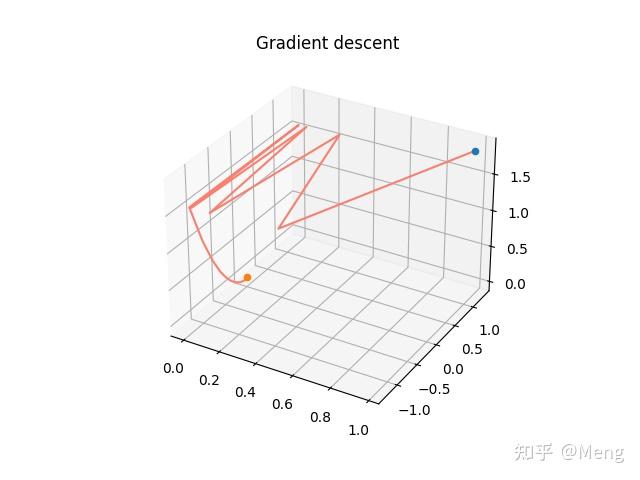
图2 GD搜索路径

对初始点敏感，不好的初始点无法收敛。
搜索效率低下，成“Z&#34;型搜索。

		自动登录	找回密码
密码			立即注册

《最优化理论》作业1.1：梯度下降法

本帖子中包含更多资源