遗传与粒子群等智能优化算法在处理等式约束时的缺陷

zt3ff3n · 发表于 2023-3-7 10:34

差不多从2013年起，多目标遗传算法NSGA2、多目标粒子群算法、多目标灰狼算法等多目标智能优化算法就火起来了，到2020年之后，又渐渐热度下降。本文在此处以蓄电池的功率和容量约束为例，简略阐述下智能优化算法在处理等式或耦合变量约束情境下的严重弊病，如何去减轻这种弊病，以及阐述下智能优化算法的优势又在哪里。至于以粒子群和遗传为首的智能优化算法，与以yalmip+cplex(gurobi)为首的数学规划算法的代码的书写区别，以及寻优方式的不同，请兄弟们自行查阅知识进行积累。
一、智能优化算法的劣势总结

（1）种群生成-择优-进化-越界约束或重新生成-进化>>>收敛，步骤繁多
（2）大量的随机个体生成，做了很多无效计算，而不是cplex的梯度下降等算法，因而计算效率较低
（3）例如粒子群优化时的速度步长等对收敛速度与粒子位置卡边界的概率等都影响较大
（4）种群大小、迭代次数的多少，即使收敛了，是否是最优很难评价（甚至有些论文写的粒子群、遗传、灰狼、鲸鱼、细菌觅食算法等的对比，即使相同的种群数量和迭代次数，也因为其中很多步长-偏好系数等参数的选取不同，而导致它们之间的对比在我看来没多大意义。例如遗传和粒子群对比，遗传的变异概率和交叉概率选多少才算公平呢？粒子群根本没这个参数，那又如何对比？难道是将遗传的变异概率和交叉概率列表法都试一个遍取其中最优的，再把粒子群的步长等参数全列表实验一个遍取最优的，然后两个最优的进行比较吗？完全没啥可比性啊。虽然这里吐槽下智能优化算法的劣势，但下面我也会阐述他的优势，各位别急着想与我争论）
（5）难以处理约束或变量很多、很复杂的问题
（6）智能优化算法难以处理等式约束问题。这个问题我想详细的展开来阐述一下：
1）若把所有可控设备的出力或负荷都用rand()生成，那么累加后，99.9%的概率是不满足电平衡等式约束的。
处理方法：把处理区间最大的设备，例如主网购售电功率上下限制内的变量C，把他用C=A1+A2+A3-B1-B2求出来，而不是用rand()生成。这里要是能把其上下限改为[-无穷，+正无穷]那就好多了。否则，只能选择设置罚函数或者是粒子重新生成或进化了。
2）针对电池这种最大放电功率、最大充电功率、初始容量、最小容量、最大容量、充电功率、放电功率、各时刻容量这些参数间的冲突难题。第一种，已知电池初始容量，用粒子群生成各时刻充放电功率，继而利用初始容量和功率累加得到各个时刻的容量，此种方法容易导致容量越上届或越下届。第二种，功率生成求容量这种方法，很容易导致最后时刻的容量不等于初始时刻的容量。第三种，已知电池初始容量，用粒子群生成各时刻容量，继而利用前后时刻容量递减得到各个时刻的功率，此种方法容易导致功率越上界或越下界。针对此类问题，我做过一次更通用的数学模型的升华，如下：
①程序实现的功能
要求随机填满一数组，已经给定了数组起始点数值A和结束点数值B，现在需要将中间各个位置补齐数。所补的数与前后数的差值P受条件( C<=P<=D )的限制，同时数组中所有的数S(i)都在上线限之中（对任意S(i)属于数组， E<=S(i)<=F ）。
②实际意义
汽车充电问题。汽车来时电量A定值，取车时电量B定值。现在需要调度电池充放电P，所以要求随机补齐数组中间的数Soc(i)(蓄电池电量)，所补的电量Soc(i)与前后数之间的差，就是充放电功率P，P需要被限制（最大放电功率<P<最大充电功率），同时，数组中所有的数S(i)都在上线限之中（蓄电池最小容量< Soc(i)<蓄电池最大容量）。
③传统算法
从初始点SOC(1)开始，随机生成P（i）,然后 SOC(i)+ P（i）=SOC(i+1),等推导到倒数第2个时刻N的电量SOC(N-1)时，判断SOC(N)-SOC(N-1)得到的P（N）是否在Pmin和Pmax之间，若是则保留，若不是则舍弃。
该算法存在的问题：当N值越大，传统算法舍弃的数组次数就越多，当N=24时，即模拟一天的电量变化时，常常需要舍弃约30000次。

图1 rand生成功率容量双约束概率极小的缺陷

④算法优化半成品
添加修正系数Correct_Factor，实现，当数组有不符合，即末端越限的趋势时，增加反向的概率，将其抢救回来。修正系数距离数组后端位置越近，常常越接近于1，修正的痕迹越明显。
当修正系数接近于1时再动作，就可以实现将本该舍弃的数组，从死亡线拉回来。但末端差值常常会斜率过大，常常不符合实际。
修正系数实时作用（从0到1都动作）。这会导致前端数组差值和后端数组差值具有明显的正负差异。且前端功率趋近于最小值，后端趋近于最大值。功率大致符合正比例递增。

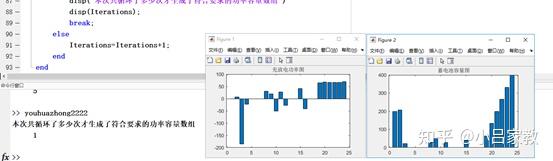
图2 功率容量双约束生成的半优化结果

⑤算法优化成品
   添加修正系数,和修正系数阈值Correct_Factor_threshold（0到1之间），修正系数阈值越小（接近0），修正作用的起始时刻越早，总次数也越多，生成的合格数组多样性也越少，但可更快速找到合格数组。反之，修正系数阈值越大（接近1），修正作用的起始时刻越晚，修正总次数也越少，生成的合格数组多样性也越多，但找到合格数组所需循环次数也越多。选择合适的修正系数阈值0.6~0.85，和轮盘赌中的方差,就可以在速度与数组多样性之间权衡，实现较为快速，较为多样。

图3 功率容量双约束生成的优化结果成品

成品代码如下：
clc
clear
%蓄电池容量为0~500
%初始电量和末端电量在0~500间先设置
%然后根据最大输出功率（负数）和最大充电功率（正数），随机生成中间各个数值
%当发现在某一时刻点越限（越限系数可以设置）时，需要之后几个必须有方向性的修正，
BA_Soc_Max=500;          % kwh
ChargeSpeed_Max=70;       % kw
DisChargeSpeed_Max=-200; % kw
%设定初始电量和末端电量,时刻点数（本程序选择为小时数）
Start_Soc=200 ;       %初始电量
End_Soc=400;          %截止电量
N_Hour=24;             %小时数（小时数为6，去掉首端末端，意思是需要再添加四组随机数）
%随机生成多组中间四个时刻的充放电功率，当末端电量，在倒数第二个电量的上下规定区间内时，说明此组随机生成的电池容量满足最大最小功率限值
BA_Soc(1)=Start_Soc ;
BA_Soc(N_Hour)=End_Soc ;
P(1)=0;
%将当前的蓄电池容量与最后时刻的蓄电池容量做差，
%第一种情况：
%差值若为正，则需要减小，就除以减小最大速率的绝对值，得到，以最大速率下降所需要的小时数。
%若这个小时数，比剩余的小时数小，则不约束方向，。反之，则约束其方向和速率为下降最大速度。
%第二种情况:
%差值若为负。同理，小变化。
%若采用上面两种方法的末端强制最大速率上升或者下降约束，虽然会把很多本该舍去的数组，强行抢救回来，但也会导致末端斜率过大，样本劣质。
%为解决这问题，可以设置提前变向概率，。也就是当发现有跑偏趋势时，根据当前修正所需最短小时数，与剩余小时数的比值（0到1之间的数值）
%比值越大，则修正方向越确定，修正步长（充放电速率）越接近最大值。
%下面上程序：
Correct_Factor_threshold=0.8; %修正系数阈值
Iterations=1;       %迭代次数
while(1)
for i=2:N_Hour-1
%       P(i)= DisChargeSpeed_Max + rand(1)*(ChargeSpeed_Max-DisChargeSpeed_Max);
      %计算修正系数时需要根据差值正负分别除以（充电或放电最大速度）
      if End_Soc-BA_Soc(i-1)>0       %大于零说明还需要充电，则修正方向偏向于加正数，
         Correct_Factor(i)= (End_Soc-BA_Soc(i-1) )/ ChargeSpeed_Max/(N_Hour-i+1 );    %修正概率
         if Correct_Factor(i)>Correct_Factor_threshold
               r(i)=normrnd(Correct_Factor(i),0.2);
               if r(i)>1
                  r(i)=1;
               elseif r<0
                  r(i)=0;
               end
               if rand(1)<r(i)
                  P(i)=r(i)*ChargeSpeed_Max;
               else
                  P(i)=(1-r(i))*DisChargeSpeed_Max;
               end
         else
               P(i)= DisChargeSpeed_Max + rand(1)*(ChargeSpeed_Max-DisChargeSpeed_Max);
         end

      else
         Correct_Factor(i)= abs(End_Soc-BA_Soc(i-1) )/abs( DisChargeSpeed_Max)/(N_Hour-i+1 );    %修正概率
         if Correct_Factor(i)>Correct_Factor_threshold
            r(i)=normrnd(Correct_Factor(i),0.2);
               if r(i)>1
                  r(i)=1;
               elseif r(i)<0
                  r(i)=0;
               end
               if rand(1)<r(i)
                  P(i)=r(i)*DisChargeSpeed_Max;
               else
                  P(i)=(1-r(i))*ChargeSpeed_Max;
               end
         else
               P(i)= DisChargeSpeed_Max + rand(1)*(ChargeSpeed_Max-DisChargeSpeed_Max);
         end

      end
      BA_Soc(i)=BA_Soc(i-1)+P(i) ;
      if BA_Soc(i)>BA_Soc_Max
         BA_Soc(i)=BA_Soc_Max;
         P(i)= BA_Soc_Max-BA_Soc(i-1);
      elseif BA_Soc(i)<0
         BA_Soc(i)=0;
         P(i)= 0-BA_Soc(i-1);
      end
end

P(N_Hour)= End_Soc-BA_Soc(N_Hour-1) ;
if  P(N_Hour)>=DisChargeSpeed_Max && P(N_Hour)<=  ChargeSpeed_Max
      figure(1)
      bar(P );
      title(&#39;充放电功率图&#39;)
      figure(2)
      bar(BA_Soc);
      title(&#39;蓄电池容量图&#39;)
      disp(&#39;本次共循环了多少次才生成了符合要求的功率容量数组&#39;)
      disp(Iterations);
      break;
else
      Iterations=Iterations+1;
end
end

%重点在于观察已下几个数据：
% （1）循环次数（也就是生成一组有效数据需要运算的次数）（多运行几次后就可以发现，未优化前，常常需要几十上百甚至上千次，但优化后只需要1到2次）
% （2）生成的数组中，P数组的随机性。（发现，修改因子虽然限制了方向和大小，但因为设置了修改因子大于0.5再修改，所以数组前期得以自动生成，即使后期修改，仍旧大致可以满足）
% （3）优化后，功率P的正负数比例仍旧大致等于充放电功率的绝对值之比。（算例选取充放电功率比为1，可以发现实际结果，正负出现次数比，也为1，功率正负时刻大致相间）
二、智能优化算法的优势总结

以市场议价为例子，必然包含电价变量乘以功率变量，这就出现了二次非平方项，yalmip+cplex就没法求解了，但是yalmip+gurobi倒是可以求解。继续，上层电网电价变量，下层多主体ADMM共享电能后的总购电功率变量，这样因为下层模型为非线性，因此这时，电价变量乘以功率变量牵扯到下层非线性即使用gurobi也没法求解了。此时，将上层电价变量用粒子群生成的常数序列替代，再带入此常数序列到下层非线性规划内与功率变量相乘，就不会出现二次非平方项了，就可以求解了，这就是主从博弈的一种，也是智能优化算法与CPLEX联合的优势。
此外，若是二次，三次，ln等变量，那么放进yalmip里线性化过程过难的，那么用智能优化算法生成的常数序列带入求解再迭代优化，也是一个小小的优势，但是我宁愿费劲去线性化，或是容许简化模型带来的误差。总之能用yalmip+cplex(gurobi)，就不用智能优化算法。
祝大家学业有成，毕业顺利！！！

		自动登录	找回密码
密码			立即注册

遗传与粒子群等智能优化算法在处理等式约束时的缺陷

本帖子中包含更多资源