|
|
课程网站 GAMES103:基于物理的计算机动画入门 - 计算机图形学与混合现实在线平台
有一些图片是从课程ppt里粘贴的,侵删。
之后有时间再更新一些关键词的提纲,用来对照关键词回忆概念。
图形学介绍
图形学的流程是:模型(几何) -> 模拟/动画 -> 渲染
这就是图形学的三大模块。
动画方向的分类以及各种方法
首先动画方向分为两种:
第一种是非物理的动画,比如人体的一些动作,比如关键帧,比如动作捕捉等等。
第二种是基于物理的动画模拟(本课的内容)
基于物理的动画模拟有以下方向。
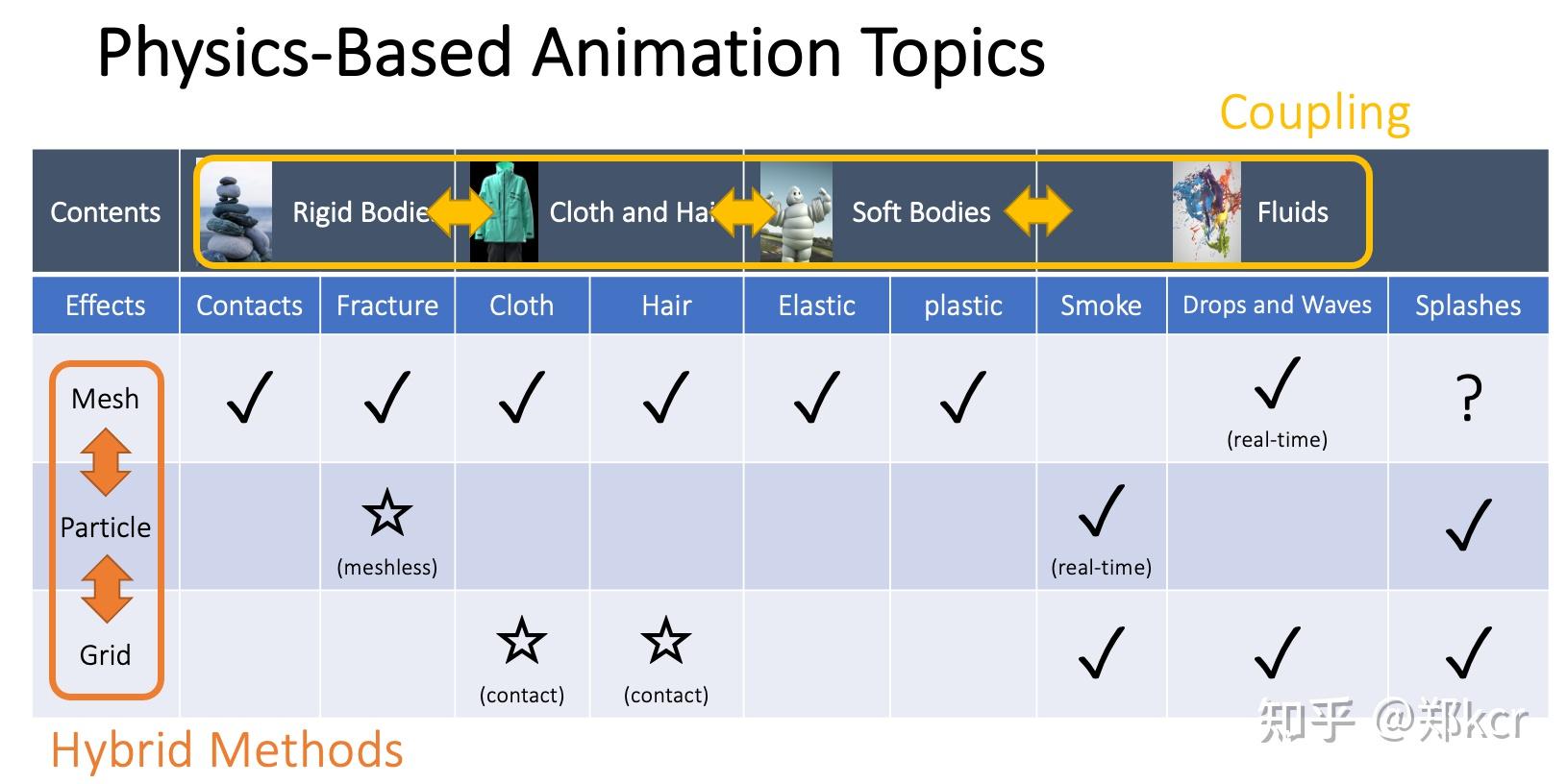
按照物体的属性来分类,主要是刚体(碰撞、破碎)、头发/布料、软物质(弹性/塑料 ),流体(烟雾、水滴/波浪,水花)
刚体的碰撞可以实时处理,破碎一般都是离线的。
头发和布料类似。
软物质的elastic deformation是指可恢复的形变,当外力为零形变也恢复。plastic deformation是指不可恢复的形变。
Are Elastic And Plastic Same | Difference Between Elastic and Plastic
按照模拟方法分类:可以使用mesh、particle或者grid来进行模拟
刚体、头发/布料、软物质一般都使用mesh来进行模拟。
烟雾使用particle(real time),也可以使用grid。
水滴/波纹还是比较完整,所以一般使用mesh(real time)。也可以使用grid,精度更高。
水花是难点,使用粒子或者grid。需要opengl或者其他工具实现,Unity做不了。
不同的方法可以混合在一起,比如MPM方法
不同的材料也可以结合在一起互相coupling。
模拟方法的一般方法论
模拟的核心,万变不离其宗。
定义状态变量 (位置、速度 或者 方向、角速度)
定义能量(弹簧能量,外界能量,strain能量)
根据能量计算出力,更新状态变量。更新的方法可以使用显式或者隐式方法。
数值方法和优化算法
Ax=b
直接求逆 x = A^{-1}b 速度太慢
有两种方法:
直接法(LU分解)
A=LU, Ly=b,Ux=y
迭代法(Jacobi Method / Gauss-Seidel Method)
\mathbf{x}^{[k+1]}=\mathbf{x}^{[k]}+\alpha\mathbf{M}^{-1}\left(\mathbf{b}-\mathbf{A} \mathbf{x}^{[k]}\right)
本质上优化方向就是最小二乘法的方向, \alpha 是学习速率, M矩阵理想的是A本身,实际上用一些近似

\mathbf{x}^{*}=\operatorname{argmin} F(\mathbf{x})
线性优化反而要求方程组之类的,有很多复杂的地方。
非线性优化虽然更难,但是因为数学家也没什么好办法,所以实现上更简单
最简单的就是gradient decent \mathbf{x}^{(k+1)} \leftarrow \mathbf{x}^{(k)}-\alpha^{(k)} \nabla F\left(\mathbf{x}^{(k)}\right)
可变步长:沿着gradient decent的方向走,不能保证下一步的函数值比当前要小,只能保证在足够小的邻域内函数值更小。Exact line search 找到最合适的 \alpha 使得下一步是最小值。Backtracking line search,不断减小步长直到下一步的函数值比当前步大。
自动可变步长:可以在gradient decent的下降方向前面乘一个矩阵
\mathbf{X}^{(k+1)} \leftarrow \mathbf{X}^{(k)}-\alpha^{(k)}\left(\mathbf{P}^{(k)}\right)^{-1} \nabla F\left(\mathbf{X}^{(k)}\right)
但是我们要保证乘上矩阵以后的方向和gradient decent方向之间的夹角小于90度。下面有几个例子

可以看到,对于Newton's method,只有当Hessian正定的时候,才能保证算法是合理的。
牛顿法:给定f(x_k),f‘(x_k),f''(x_k),拟合出二次函数,然后求这个二次函数的最低谷,作为新的x。
这个二次函数的形式是 f(x)\approx f(x_k) + f'(x_k)(x-x_k) +f''(x_k)\frac{1}{2}(x-x_k)^2
最低点是对x导数为零 0=f^{\prime}(x) \approx f^{\prime}\left(x^{(k)}\right)+f^{\prime \prime}\left(x^{(k)}\right)\left(x-x^{(k)}\right)
解得 \Delta x = x^{(k+1)} - x^{(k)} = -\left(f^{\prime \prime}\left(x^{(k)}\right)\right)^{-1} f^{\prime}\left(x^{(k)}\right)
刚体
运动学模拟(第三节课)
刚体的自由度只有位置和朝向,在代码里保存位置、速度,方向、角速度。
物理信息包括质量、转动惯量、外界的力和力矩
速度通过外力改变。角速度通过力矩除转动惯量改变。
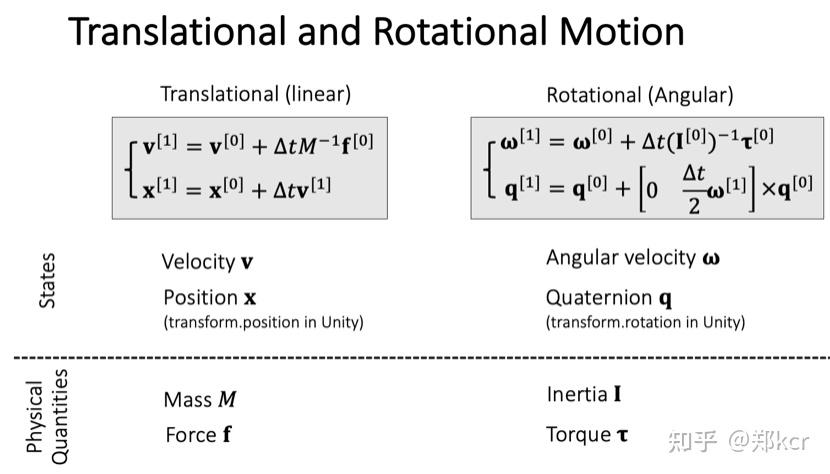
\frac{dv}{dt}=\frac{F}{m} , \frac{d\omega}{dt}=I^{-1}\tau
我们保存的状态是刚体质心的位置、速度,朝向、角动量。
对于每个质点计算出力,算出其作用在质心上的合力、合力矩来更新质心的状态。
合力好算,合力矩稍微复杂。因为需要质点相对于质心的位置,这个需要用朝向来算。转动惯量,首先保存mesh在正向的矩阵,然后通过朝向得到当前的转动惯量。
转动的描述使用四元数。
矩阵的缺点是自由度太多,转动只有三个自由度。欧拉角是随体转动角,缺点是可能出现万向节死锁。
四元数有1,i,j,k四个分量。
\left\{\begin{array}{l} \mathbf{q}=\left[\begin{array}{ll} \cos \frac{\theta}{2} & \mathbf{v} \end{array}\right] \\ \|\mathbf{q}\|=1 \end{array}\right.
theta是转动角度,v是转轴。可以映射到一个转动矩阵。
我们用四元数q代表刚体的朝向。
角速度用一个三维向量描述,方向代表转轴,大小代表转动角度。
\left\{\begin{array}{l} \boldsymbol{\omega}^{[1]}=\boldsymbol{\omega}^{[0]}+\Delta t\left(\mathbf{I}^{[0]}\right)^{-1} \mathbf{\tau}^{[0]} \\ \mathbf{q}^{[1]}=\mathbf{q}^{[0]}+\left[\begin{array}{ll} 0 & \frac{\Delta t}{2} \boldsymbol{\omega}^{[1]} \end{array}\right] \times \mathbf{q}^{[0]} \end{array}\right.
这就是角速度以及朝向的更新方式。第二个公式的乘法和加法都是quaternion的运算。
刚体碰撞(第四节课)
一般使用signed distance function
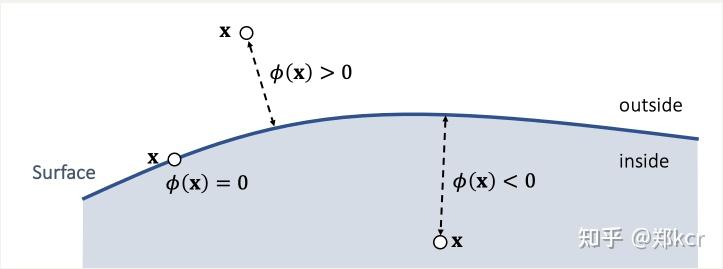
如果刚体的mesh里有顶点x的位置使得 \phi(x)<0 ,这个顶点就和表面发生了碰撞。
Signed distance function交集是求max,并集近似为求min。
当前帧发现mesh有顶点在表面内,需要进行响应。
第一种方法Penalty method:假设表面内部是一个弹性体,Quadratic penalty method能量就是 \frac{1}{2} k\phi(x)^2

也可以在表面加一个厚度为epsilon的外壳,这样物体如果进入受到的反弹力就更大。这样就不容易出现penetration issue(游戏里有时候会穿模)

Quadratic penalty method容易出现overshooting的问题(当前帧进入太深,下一帧飞出屏幕)。所以一个变种是log-barrier penalty,能量是 \rho\log (\phi(x)) ,力是 \mathbf{f} \longleftarrow \frac{\rho}{\phi(\mathbf{x})} \mathbf{N}
第二种方法 Impulse method
不定义能量,而是假设物体的状态发生一个人为设定的突变。
\mathbf{x}^{\text {new }} \longleftarrow \mathbf{x}+|\phi(\mathbf{x})| \mathbf{N}=\mathbf{x}-\phi(\mathbf{x}) \nabla \phi(\mathbf{x})
\text{if } v\cdot N < 0 , \text{then }\left\{\begin{array} { l } { \mathbf { v } _ { \mathbf { N } } \leftarrow ( \mathbf { v } \cdot \mathbf { N } ) \mathbf { N } } \\ { \mathbf { v } _ { T } \leftarrow \mathbf { v } - \mathbf { v } _ { \mathbf { N } } } \end{array} \Rightarrow \left\{\begin{array}{l} \mathbf{v}_{\mathbf{N}}^{\text {new }} \leftarrow-\mu_{\mathrm{N}} \mathbf{v}_{\mathrm{N}} \\ \mathbf{v}_{\mathrm{T}}^{\text {new }} \leftarrow a \mathbf{v}_{\mathrm{T}} \end{array} \Rightarrow \mathbf{v}^{\text {new }} \leftarrow \mathbf{v}_{\mathrm{N}}^{\text {new }}+\mathbf{v}_{\mathrm{T}}^{\text {new }}\right.\right.
刚体的质心位置、速度、朝向、角速度已知。
碰撞检测就是对当前mesh每一个顶点的位置进行检测 \mathbf{x}_{i} \longleftarrow \mathbf{x}+\mathbf{R} \mathbf{r}_{i}
碰撞响应,一旦发生碰撞,就处理所有碰撞的顶点。
Penalty method,质点i发生碰撞响应之后,把顶点的力和力矩换算成作用在质心上,更新质心状态变量。
Impluse method,质点i发生碰撞响应之后,顶点的速度发生瞬间改变,把这个冲量或者角冲量换算成作用在质心坐标上。(?这里有个问题,质点坐标改变以后怎么处理,多个质点的坐标改变怎么样叠加在质心坐标上,可能这些质点各自的改变会改变刚体的形状。在slides的作业implementation details里讨论了一下,这里坐标的更新是一个带constraint的更新情况。如果有多个质点都碰撞的话,我们可以取平均值,而不应该使用相加。)
非物理的近似方法。
把所有质点正常的更新,然后根据质点的新位置,拟合一个最好的刚体位置。
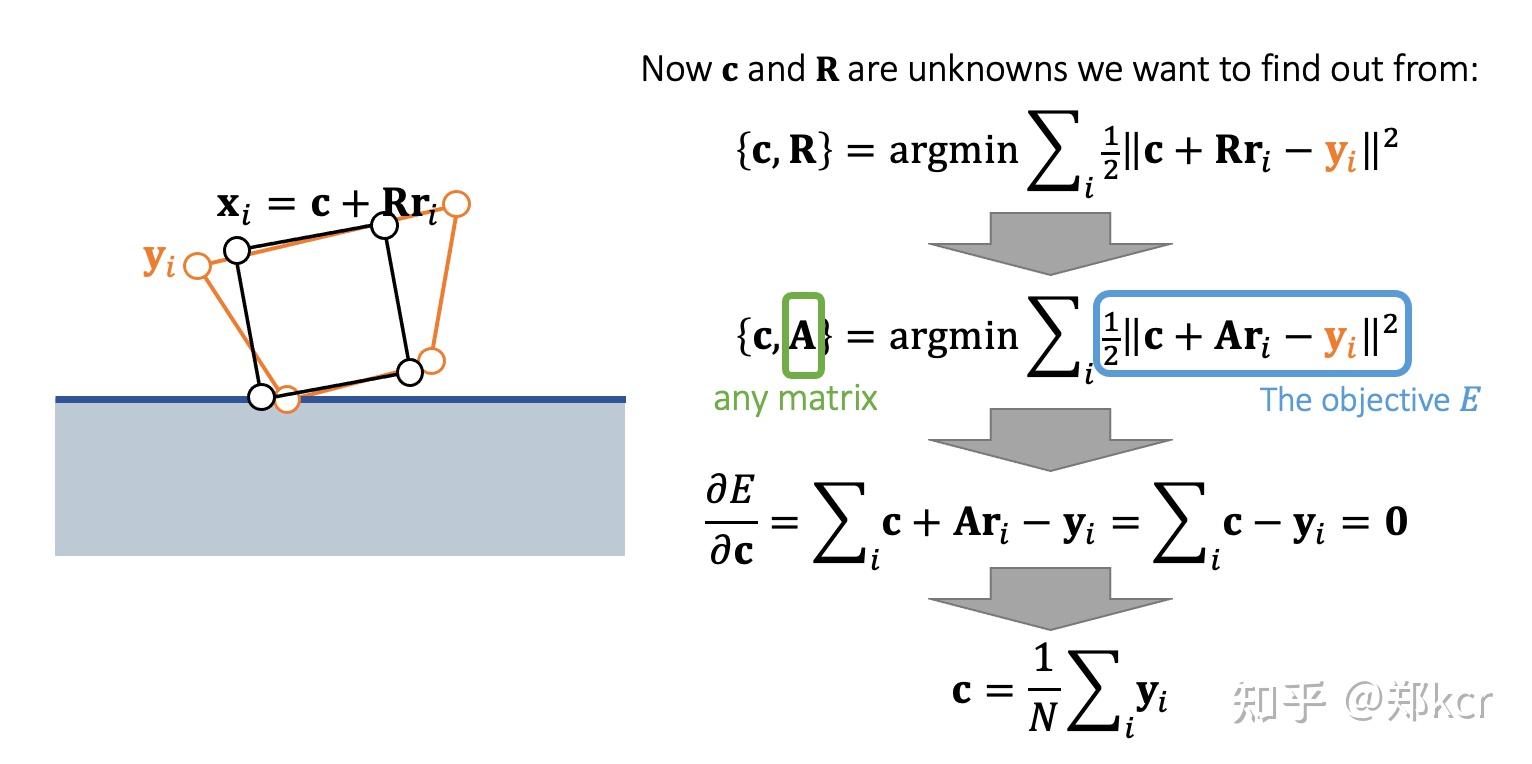
原本有约束的旋转矩阵(正交矩阵)的优化,现在使用任意矩阵A,再对A进行Polar decomposition。
Polar decomposition本质上是把线性变换拆成原地形变和旋转
\mathbf{A}=\mathbf{U D V}^{\mathrm{T}}
\mathbf{A}=\left(\mathbf{U V}^{\mathrm{T}}\right)\left(\mathbf{V D V}^{\mathrm{T}}\right)
类比负数的 x = \rho e^{i\phi} ,其中旋转矩阵可以用李代数写成exponential的形式,而形变矩阵对应 \rho



布料 (弹簧系统) 模拟
模拟方法
弹簧系统的模拟其实比较简单。
在规则的网格里添加下面的这些弹簧。其中间隔一个的弹簧是为了防止布料可以自由折叠。
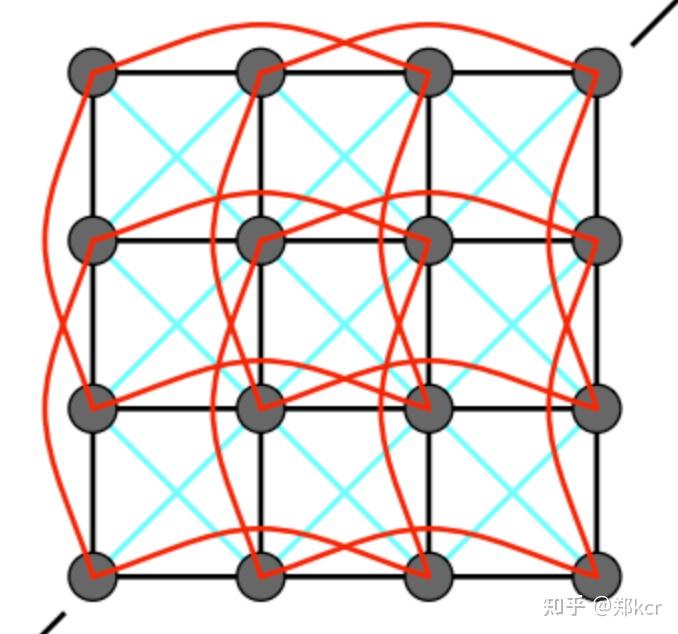
对于不规则的网格,也可以类似的处理。
弹簧的能量/哈密顿量,就是正常的胡克定律。
根据能量算出力,然后更新。
更新方法可以是显式或者隐式的。

显式积分需要Edge list, Edge length list,mass;然后每个粒子的位置和速度作为状态变量
中间变量就是每个顶点受到的力。
显式积分的问题是算法稳定性不好,容易出现overshooting,只能减少步长。

隐式积分需要求解这个方程,是一个非线性优化。可以使用牛顿法迭代求解。

这个表达式有点问题,里面的x[0]其实是x[k],然后delta x 是x[k+1]-x[k]
隐式积分的问题:Spring Hessian在一维是正定的,但是二维三维不是正定的(因为相同的能量可能对应两个构型,一个弹簧可以向上弯曲也有可能向下弯曲),所以不能保证收敛。
有一些论文讨论如何解决,比如可以修改Hessian的项。
求解上面的线性方程组可以使用迭代法 Jacobi method
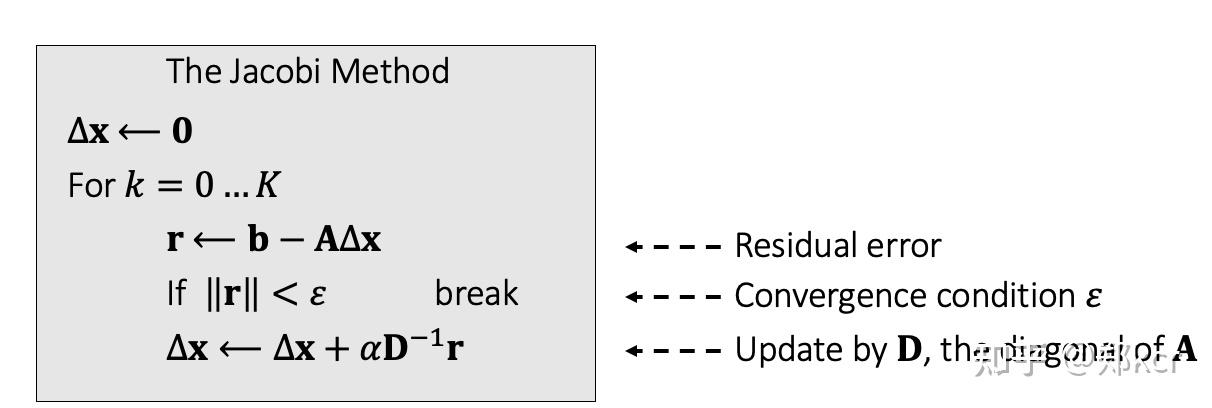
Bending and Locking issues
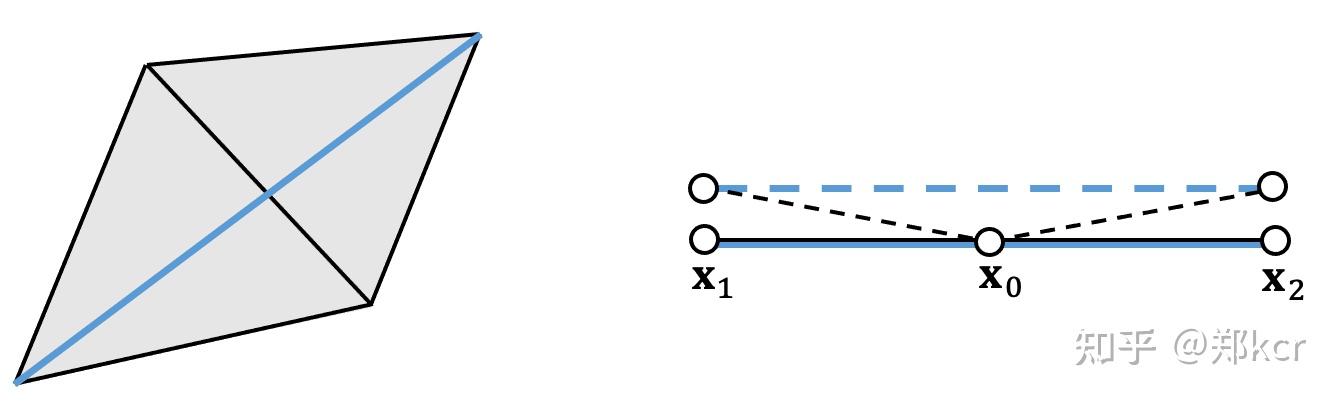
在布料接近平行的时候,上面的模型提供的弯曲的阻力非常小。这个叫做Bending issue
可以使用dihedral angle model 或者 Quadratic Bending Model 定义新的bending forces(略)。
Locking Issue就是说由于我们添加了很多根弹簧,在弹簧阻力很大的时候,对应方向的自由度被固定了。为什么我们想要阻力很大呢?因为实际的布料在平面上扯这块布,阻力是非常大的,但是同时对于bending应该是很柔软的,两者很难得兼。所以在我们的模型里 bending和stretching没法独立的处理。
这是一个本质难的问题。当弹簧阻力太大的时候布料显得僵硬,布料柔软的时候就会延展性很好更像橡皮布。
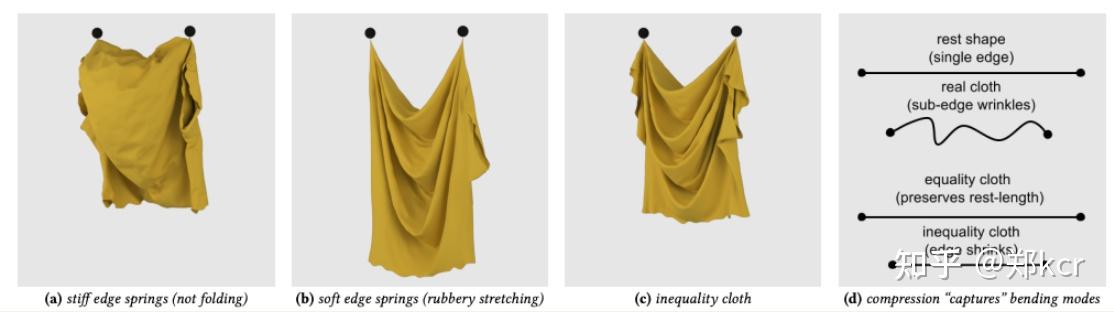
Shape matching
非物理的方法。
三角形的可以用一个3x2矩阵来描述。对这个矩阵进行polar decomposition,分解为原地scaling和rotation。
定义能量
定义能量关于scaling是个二次函数。然后我们固定R为常数。这样能量关于坐标x是个二次函数(三维弹簧不是一个二次函数,有根号之类的项),比较好处理。
本质上是Projective Dynamics,见第六讲
布料 Constraint approaches
之前提到布料如果增加stiffness,那么弹簧的劲度系数就很大。会产生locking issue。而且数值算法无论隐式还是显式积分都会不稳定。解决办法是使用正常的劲度系数,但是增加cosntraint。
Position Based Dynamics(PBD)
PBD的想法很简单,首先正常模拟,然后把位置按照比例投影到距离为原长。

但是当有多根弹簧的时候,我们如何投影?
两两投影,依次找一个pair进行投影。

这种投影方法,永远不可能严格满足constriant。
迭代的次数越多延展性越差。
两两投影的顺序会影响收敛速度和结果,可能会有顺序产生的bias。
对所有pair都进行投影,把新得到的n个顶点坐标和之前的顶点坐标做interpolation。好处是和顺序无关。坏处就是收敛速度变慢。

PBD

stiffness是非物理的实现。通过迭代次数和网格resolution控制最后是否严格满足constraint引入弹性。
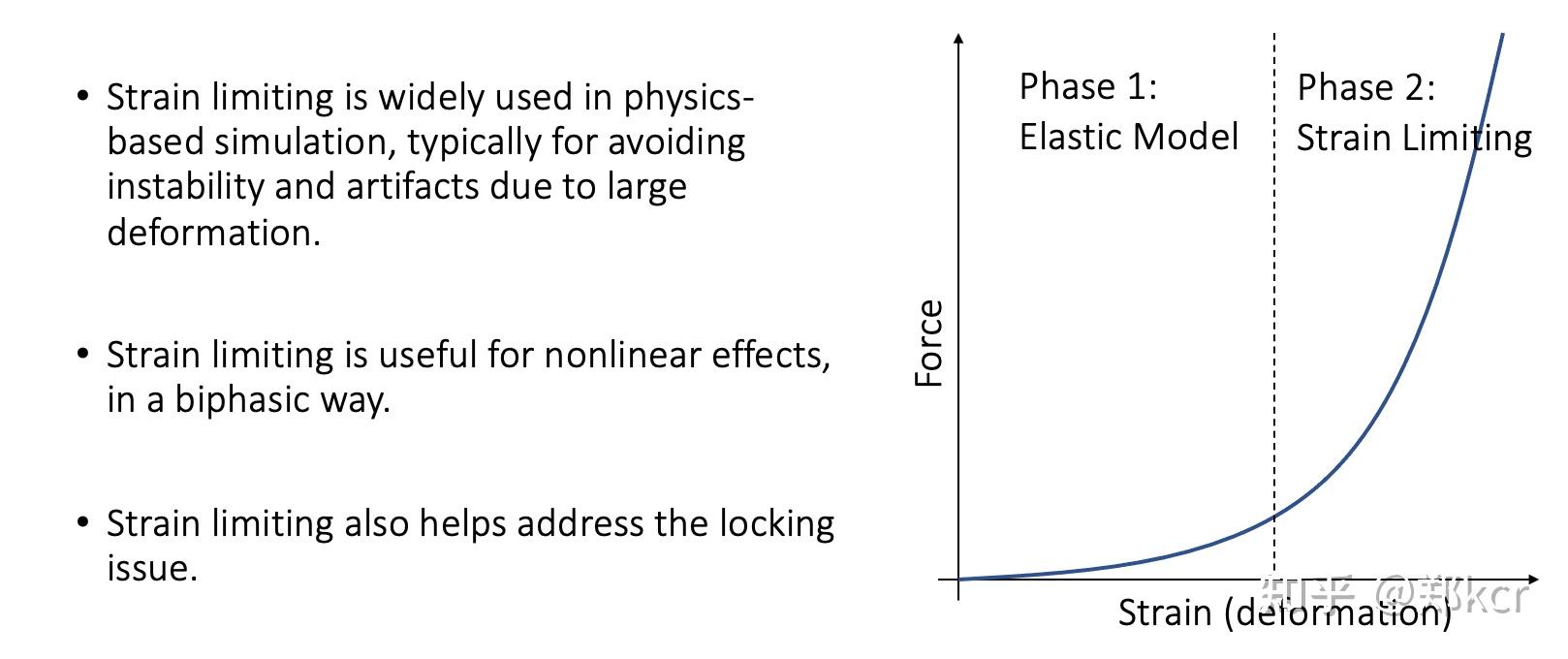
Strain limiting
这个方法就是上述的改进。
之前都投影到原长。
现在是投影到原长的某个倍数,比如(0.95,1.05)之间。其余步骤都一样

为什么叫strain limiting? 这里弹簧缩放的倍数stretching ratio叫做strain。stretchign ratio为1的时候无形变,为其他数的时候有形变,相当于是形变的一种描述。我们把strain进行了限制就是strain limiting。
也可以用三角形面积进行strain limiting。三角形面积比例开根号,再通过重心坐标进行缩放。
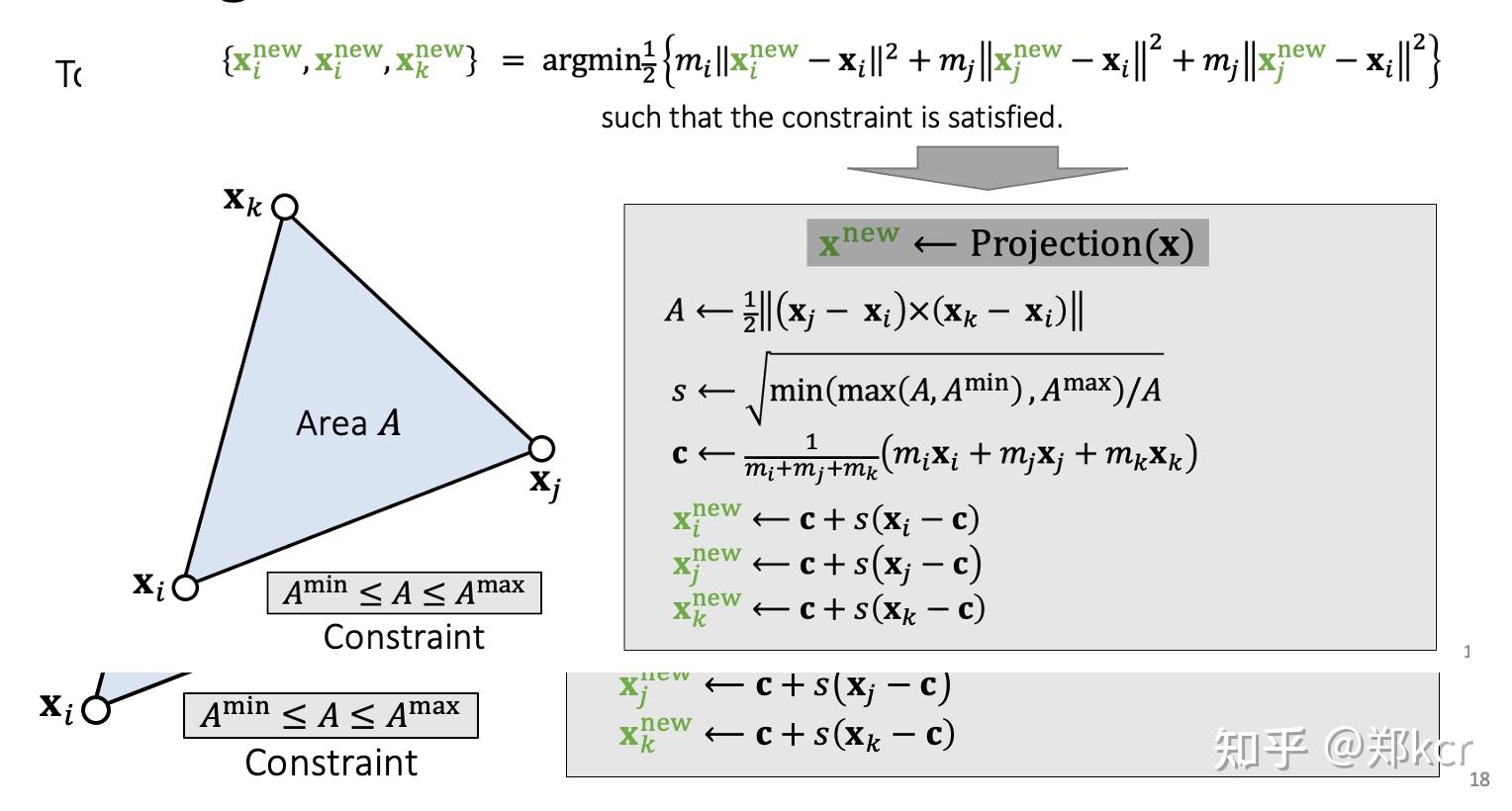
可以把strain limiting和Elastic model(之前讲的弹簧网格)结合使用。布料在小形变是弹性的,大形变是扯不动的。
Projective Dynamics
简单介绍一下。
本质上是projection的一种使用方式。

先正常模拟得到x_i,x_j。然后进行投影得到new的坐标。定义一个二次能量,这个能量使得最终的坐标接近投影后的结果,但也不是完全相等,从而近似的满足constraint。
好处是得到的二次能量的Hessian是个常数。(一般弹簧的Hessian形式复杂)就可以用这个能量进行一般的隐式计算。
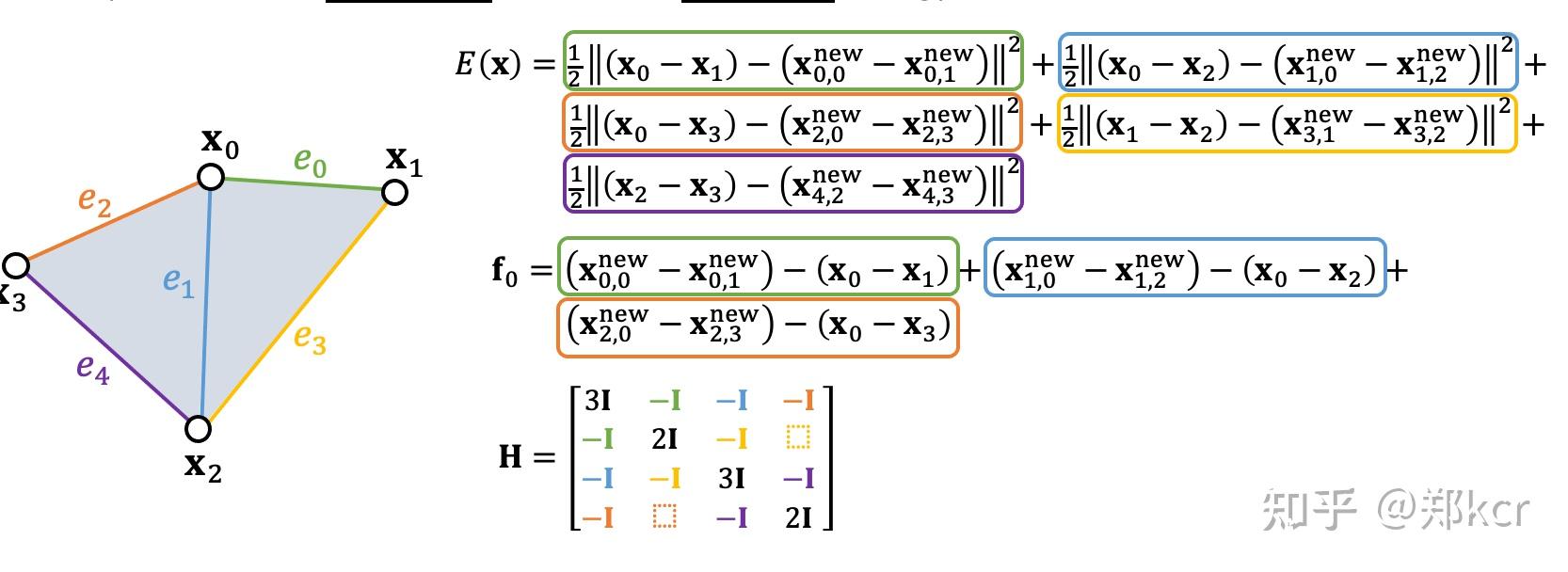
数学上这个方法叫做preconditioned steepest descent。用来近似Hessian。
Constraint Dynamics
略,定义了一个新的状态变量lambda。可以用在Articulated Rigid Bodies (ragdoll animation) 人体模拟。
Physics-Based Animation学习记录--Constraint Approaches----Constrained Dynamics 强约束问题的处理方法 - Eric的文章 - 知乎 https://zhuanlan.zhihu.com/p/473473340

布料(碰撞检测与响应)第九讲
冰点蓝:GAMES103 Lecture 08 Intro to Physics-Based Animation -Collision Handling
http://www.designartj.com/ch/reader/download_pdf_file.aspx?journal_id=bzgcysb&file_name=3618E016C89268EC5BE49414EEAFA92CB53D69655D08E5174753FBA88B67B54B3F8D784C32E993DFD7118FCC5C762CD7F1B172BB368D45E32A6253BE913D42C7&open_type=self&file_no=20211403
以及课后阅读
布料的碰撞检测与响应是最复杂的。
碰撞检测
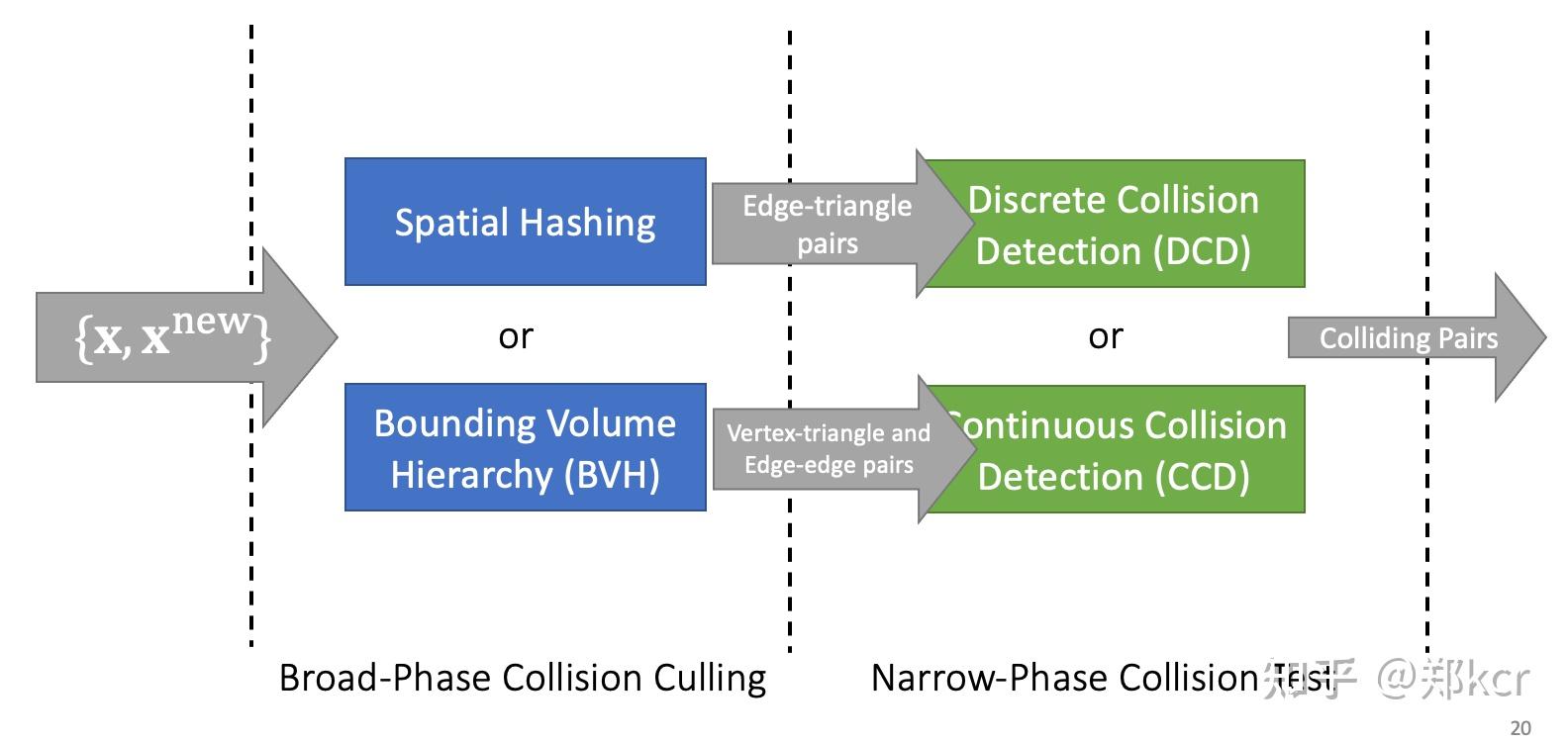
碰撞检测分为Broad-Phase检测和Narrow-phase collision test。
考虑两个mesh的碰撞检测,由于mesh有很多顶点,两两判断运算量太大,所以先通过一些数据结构大致判断一些哪些顶点可能产生碰撞,得到Pair Candidates
再进行严格的pair collision detection,分为Discrete Collision Detection(DCD)和Continuous Collision Detection(CCd)。
把关键划分为格子,格子里保存所有与之相交的三角形。然后对于每个三角形判断一下,它所在的格子里还有哪些三角形。
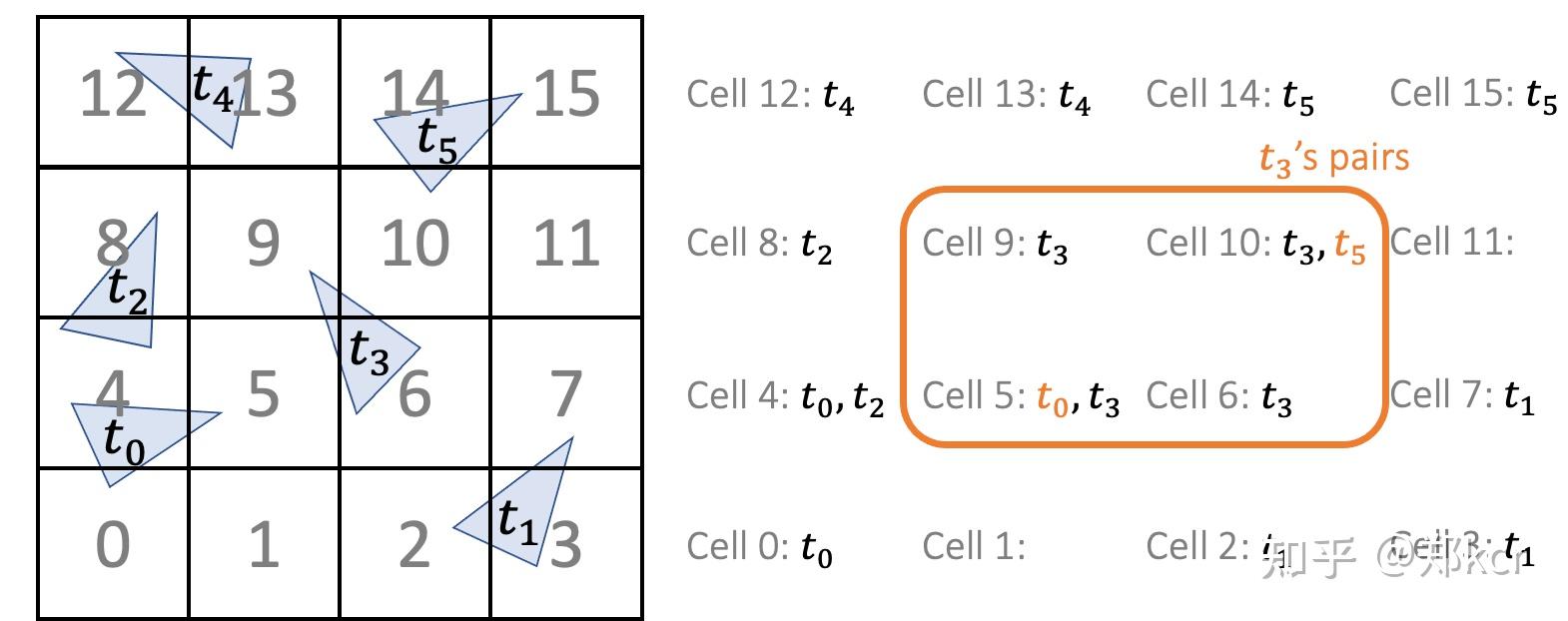
更好的做法是使用Mortion Code对格子进行编号,使得相邻的各自有相近的编号。比如这里第0和第4格子编号查了4,但是空间上相邻,这就不太好。
- BVH (Bounding Volume Hierarchy)
先把物体放到AABB里,然后再依次放入更大的AABB,构建tree的结构。
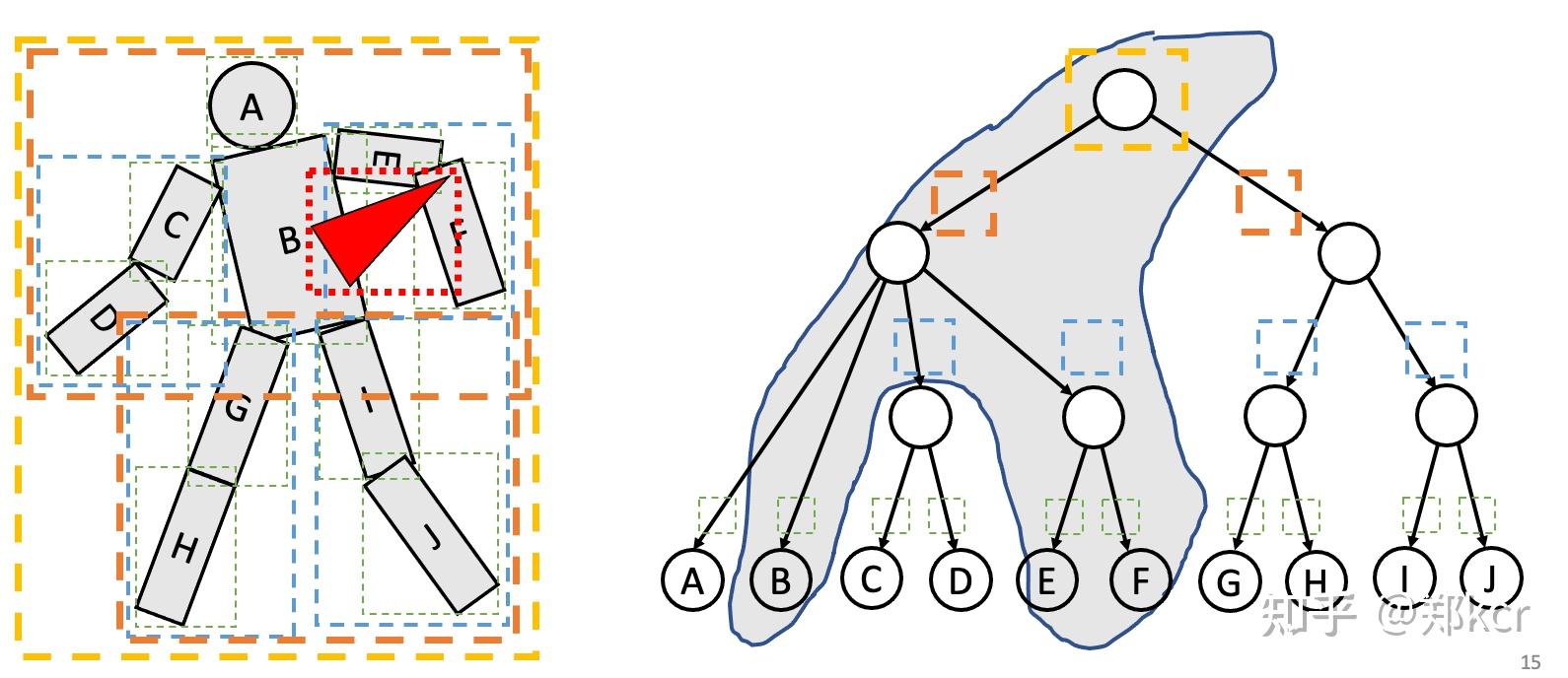

除了两个物体的相交以外,有时我们还要考虑自相交。
- Discrete Collision Detection(DCD)
核心是edge-triangle intersection,这个很简单了。通过体积先计算交点的参数t,再判断是否在三角形内。
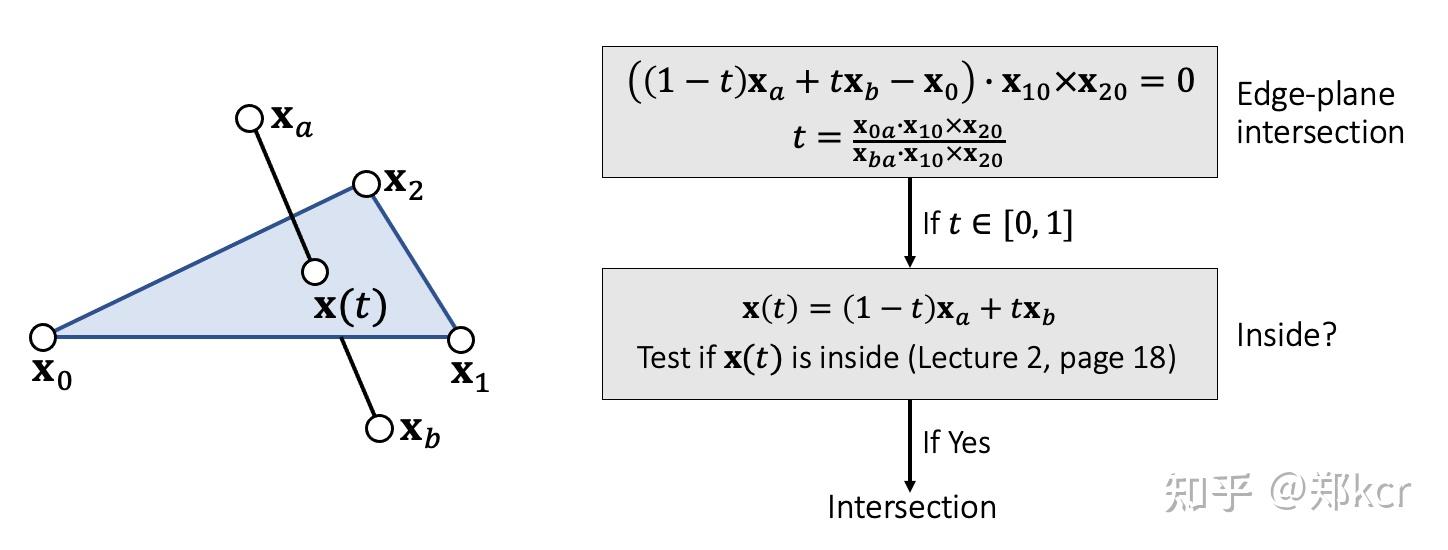
可以判断当前帧,有没有发生edge与三角形的相交。但是不能判断两帧之间有没有相交发生(Tunneling problem),所以需要减少时间步长。
- Continuous Collision Detection(CCD)
首先是判断两帧之间有没有发生vertex-triangle collision。假设有两帧的x_3 以及三角形x_0,x_1,x_2的位置,通过linear interpolation可以得到它们的轨迹。然后首先求解是否有t时刻x_3在三角形平面内,通过体积。
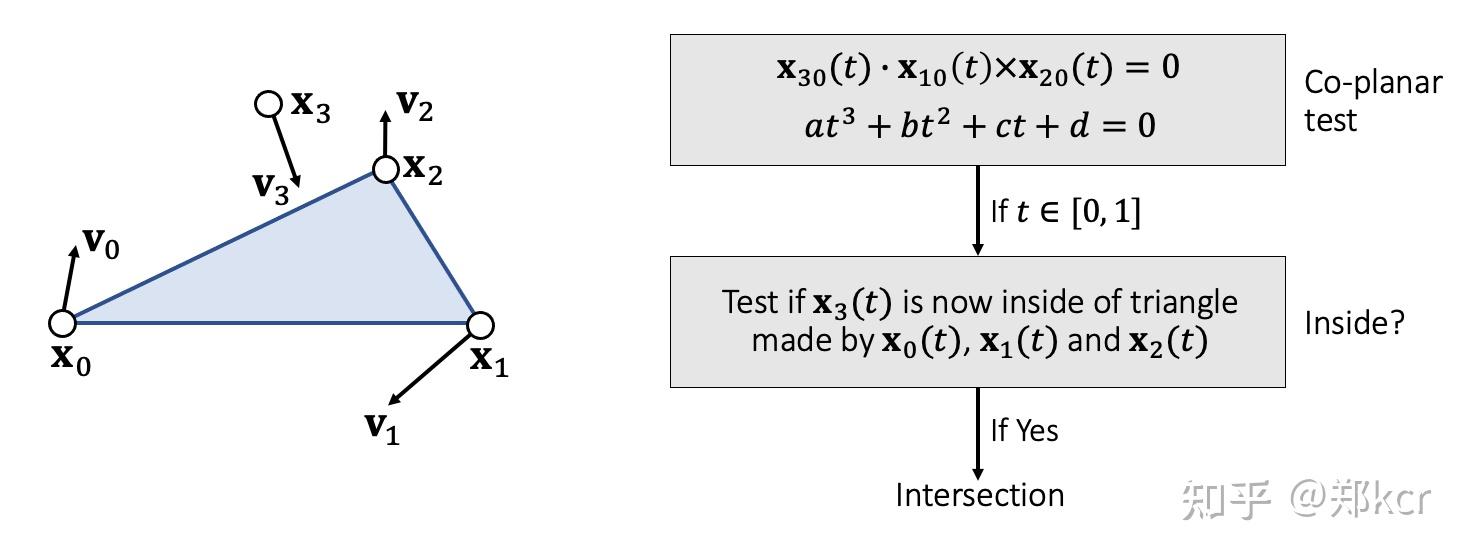
然后判断edge-edge detection
判断x_2,x_3 是否和 x_0,x_1相交,当发生相交的时候,两个edge共面,所以还是用四面体体积判断
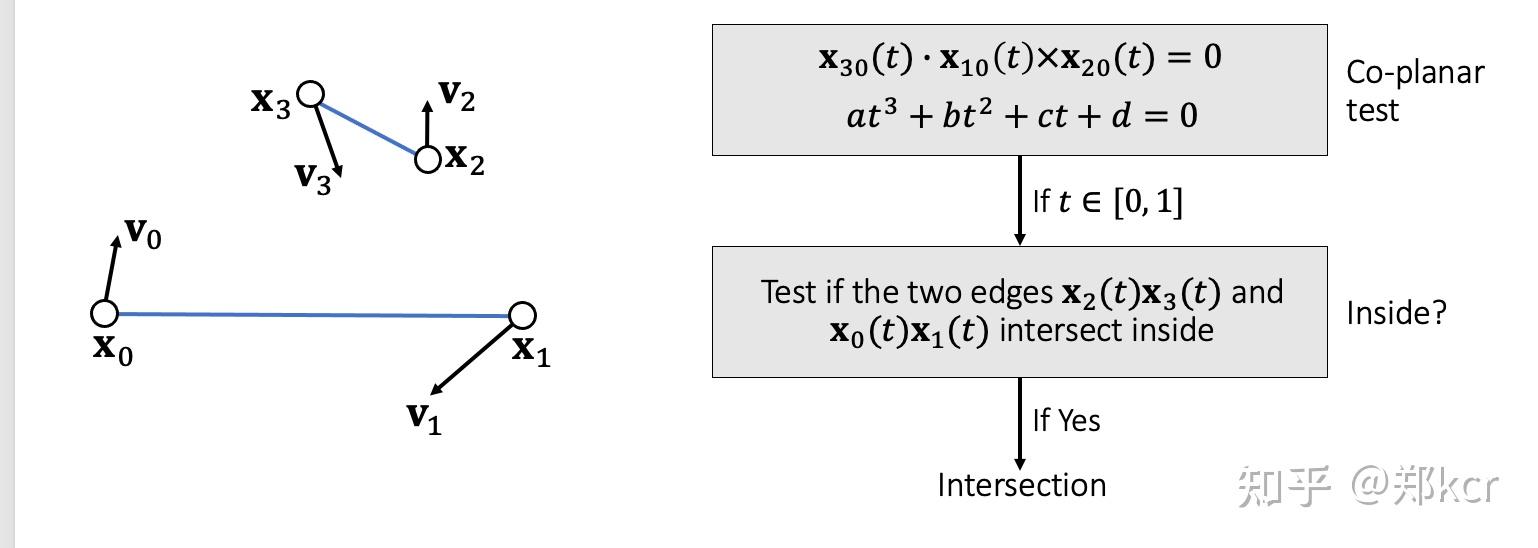
总的来说,这两个detection都要做,如果只判断vertex-triangle,可能会发生edge-edge collision。如果只判断所有edge-to-edge collision,那么顶点还有可能穿过三角形的内部(不是edge的区域)。
碰撞处理 (CCD)
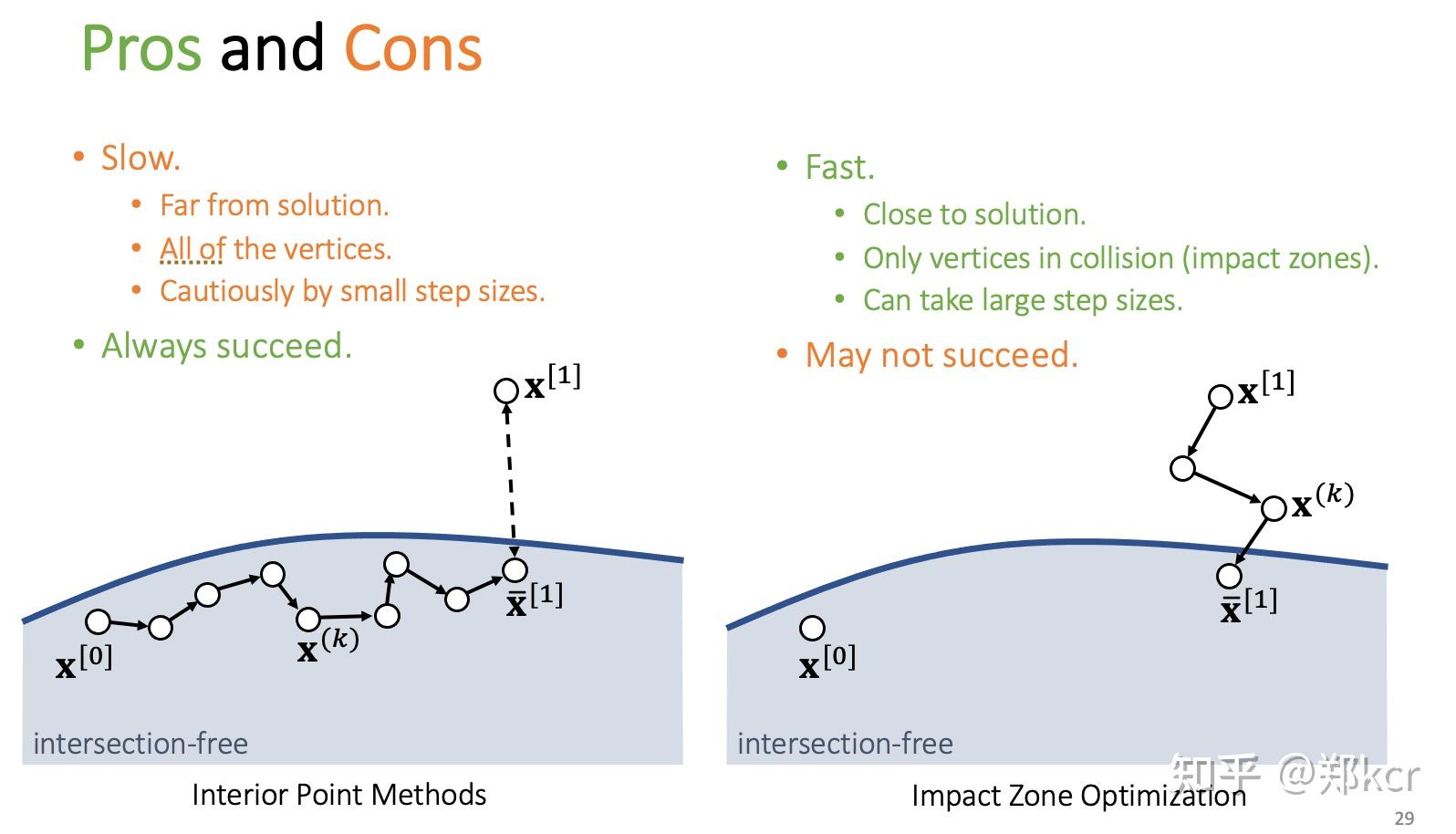
对于CCD,有两种方法,Interior Point Methods和Impact Zone Optimization。
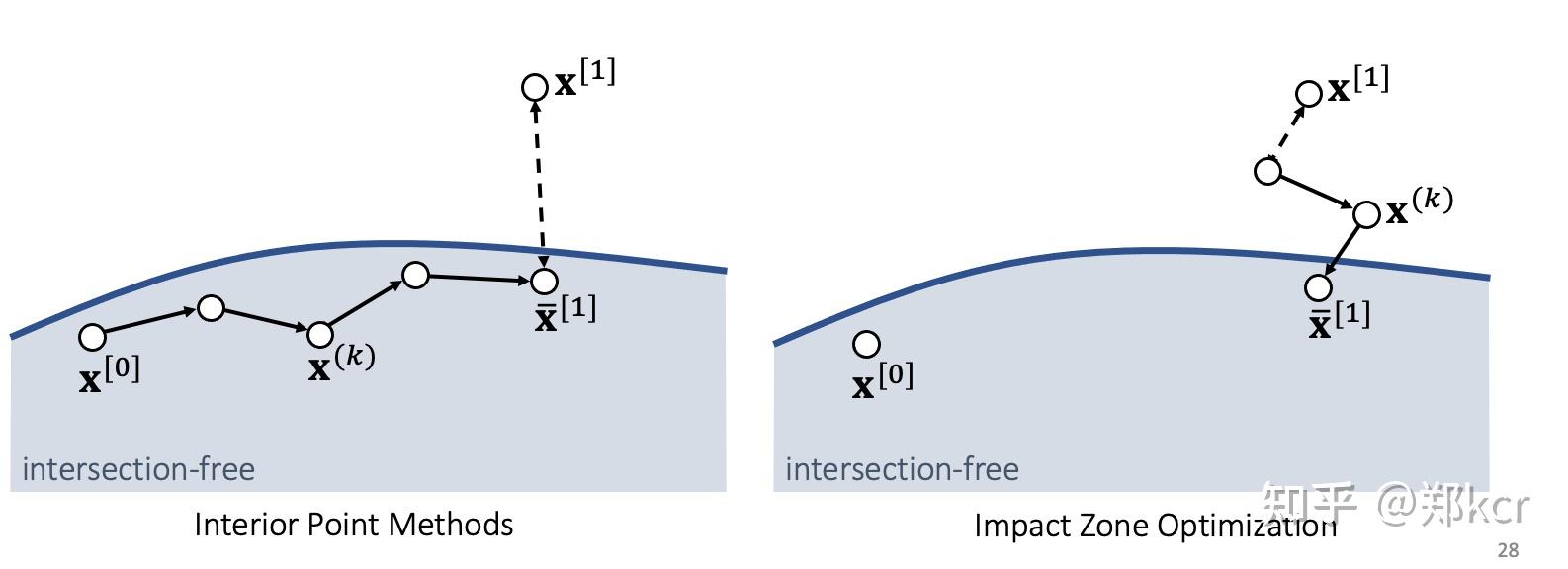
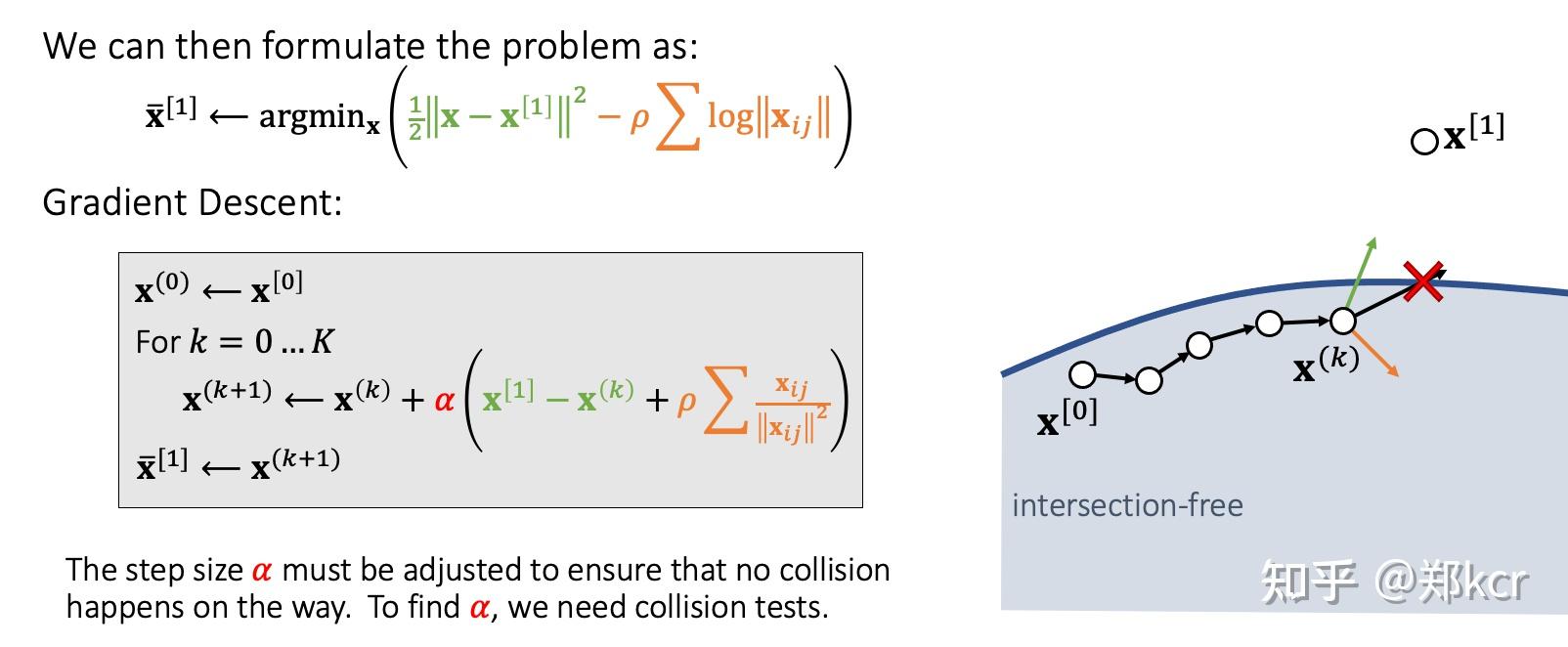
如果发现某一个顶点下一帧的位置发生了碰撞(DCD还是CCD),那么就重新跑模拟,从x[0]出发,增加一个penalty使得下一步的顶点在平面内部。比如能量使用Log-barrier,要求新的点和原始模拟结果尽可能接近,但是添加一个顶点到平面的排斥力(我的理解不知道这里ij都是什么,不过i应该是当前的顶点,j是穿越过的三角形的顶点,对j求和)

要求x[1]使得不发生碰撞,并且尽可能和原始模拟结果接近。这个方法是从x[1]出发不断的更新,直到不发生碰撞。
略
如果发生了碰撞就把那些顶点固定在物体表面。
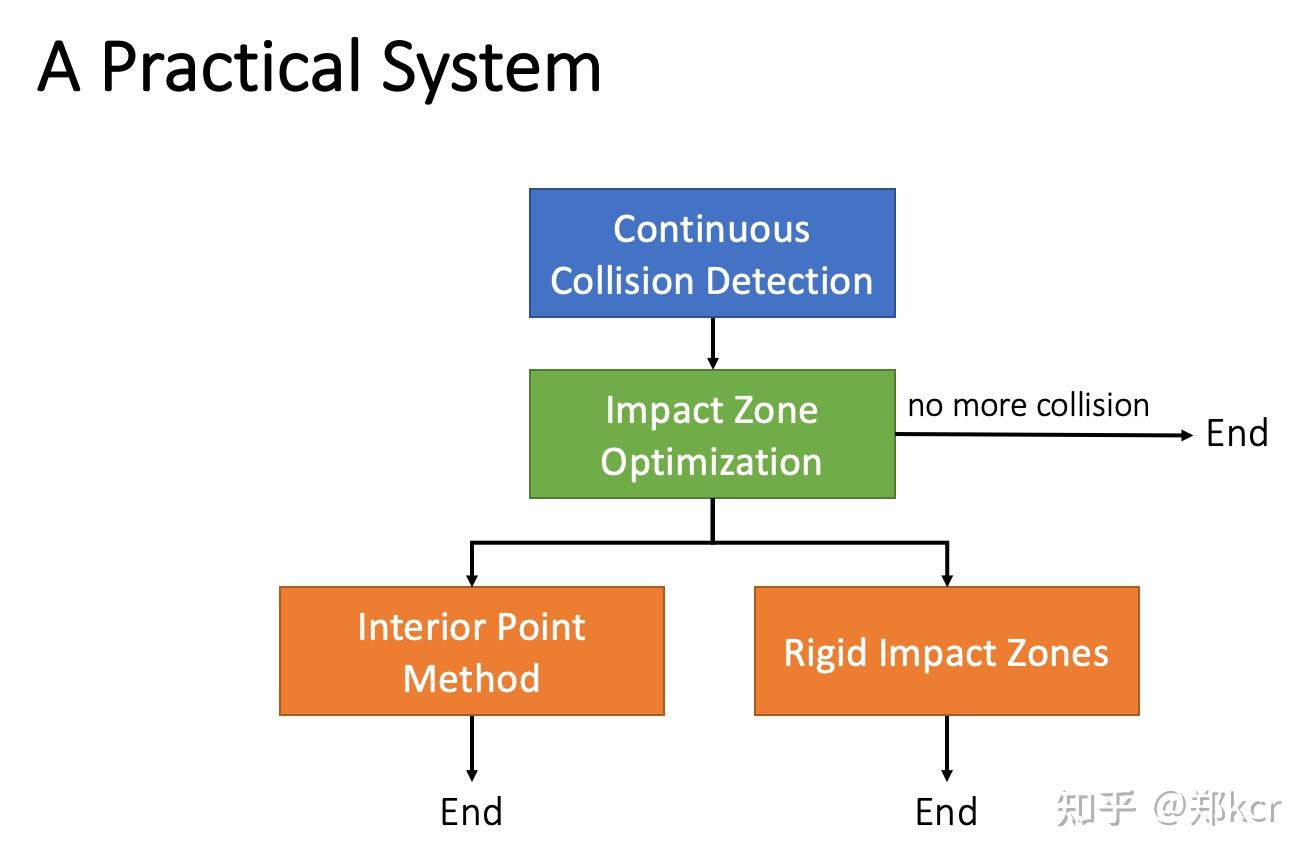
Cloth Untangling (DCD的碰撞处理)
cloth-volume或者volume-volume的碰撞处理很简单,可以把它沿着法线往外推
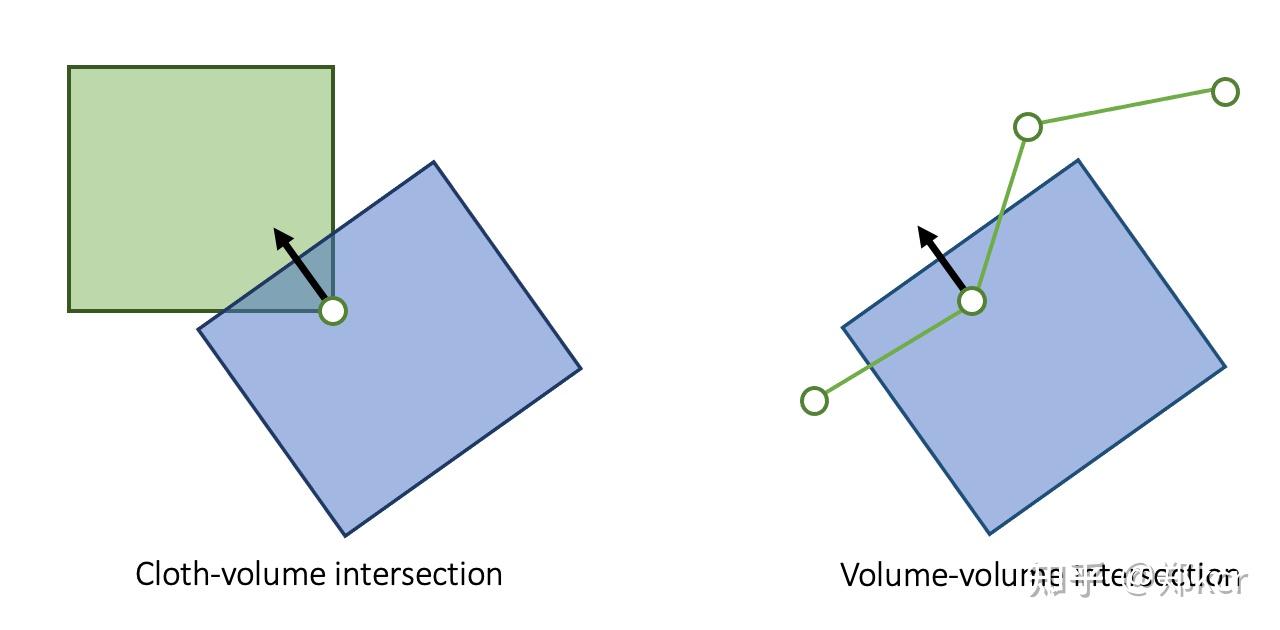
但是cloth-cloth碰撞这个问题很难解决。
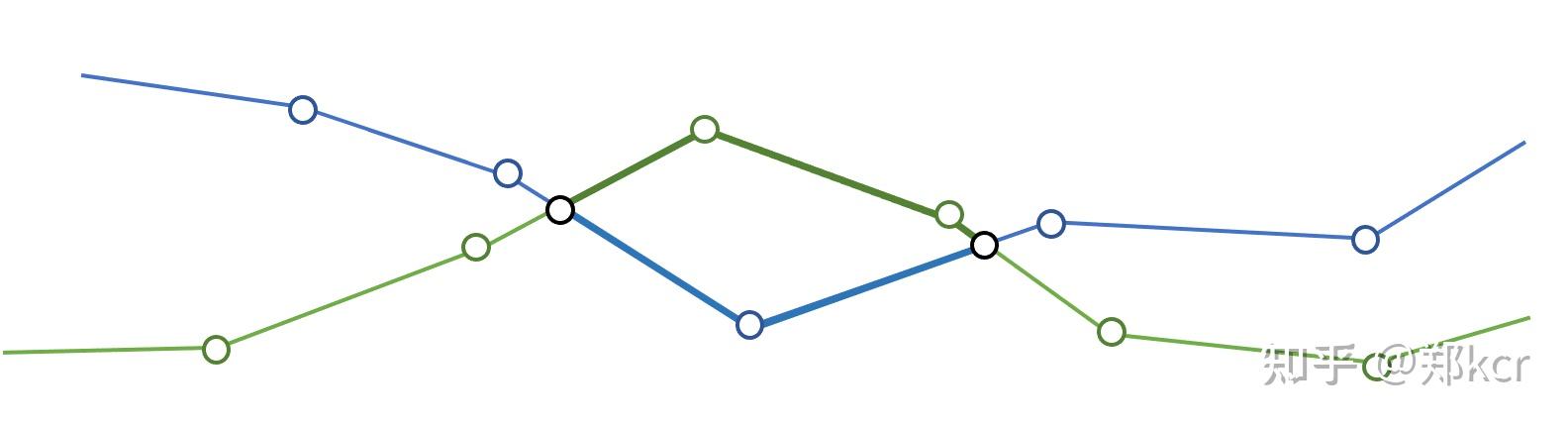
比如可以不断的把绿色的点蓝色移直到不相交
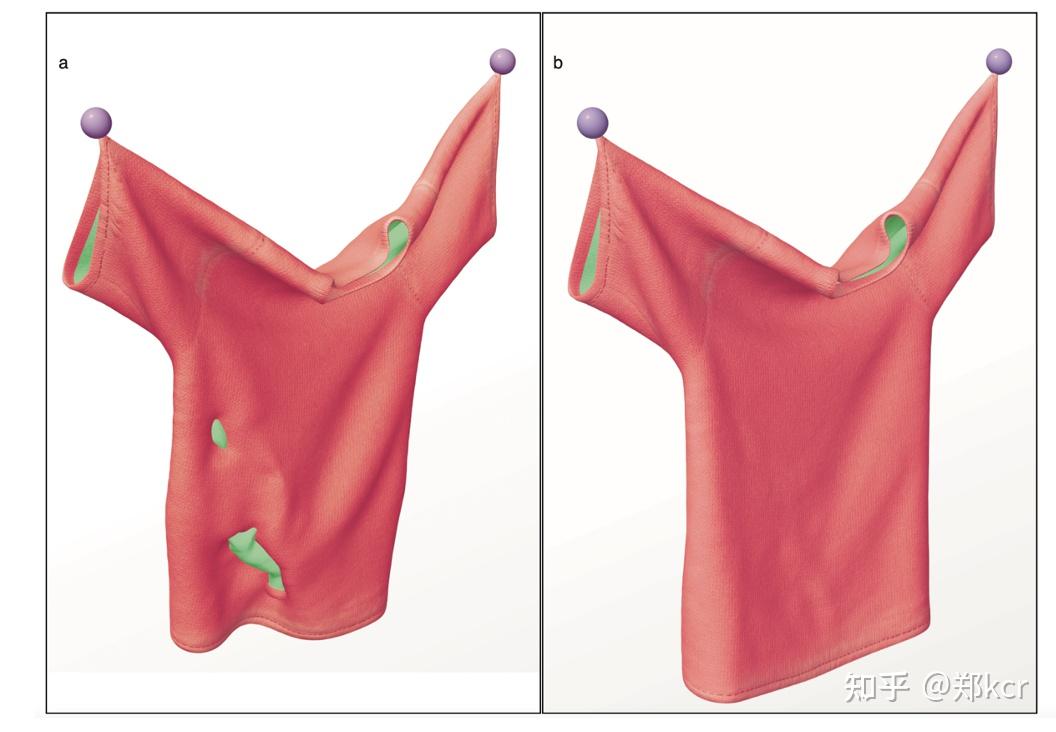
总结

有限元 (弹性体模拟)
线性有限元 Linear Finite Element Method (FEM)
什么叫线性有限元,当三角形顶点进行了某个线性变换,内部点也都进行相同的对应的线性变换。(把重心坐标相同的点映射到对应点。)
本质上也是给出一个能量,计算力。
Strain: 三角形从当前位置到下一位置表述为一个矩阵的线性变换,线性变换通过SVD拆成旋转->形变->旋转。只有第一个旋转和形变对于最终的形变有影响。定义Green strain
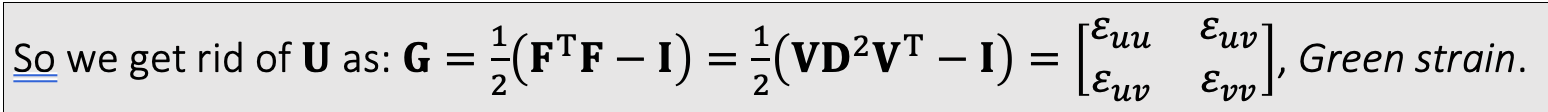
这就是一个strain,strain也就是说当形变为零G为零,当形变越大/越小,G越大/越小。
能量的形式:能量是Strain的函数,并且在三角形内为常数,所以是面积乘某个strain的函数。
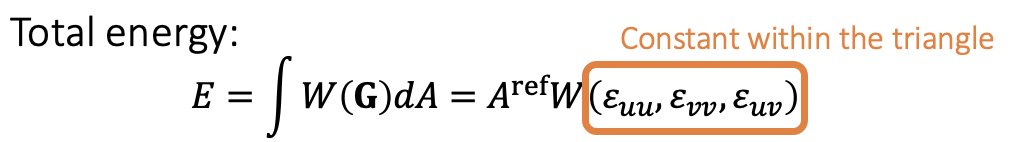
图形学常用 StVK

接下来要求每个顶点的力,其实就是对能量求导。
求导链式法则的几个中间变量。对Strain求导是Second PK stress tensor
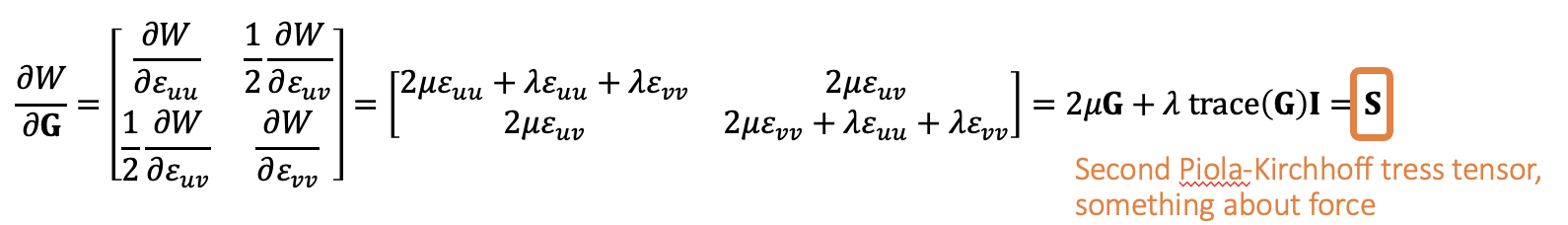
线性变换矩阵
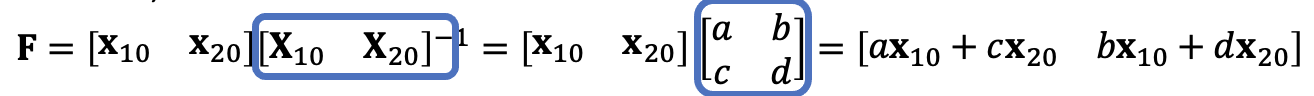
最终力的形式
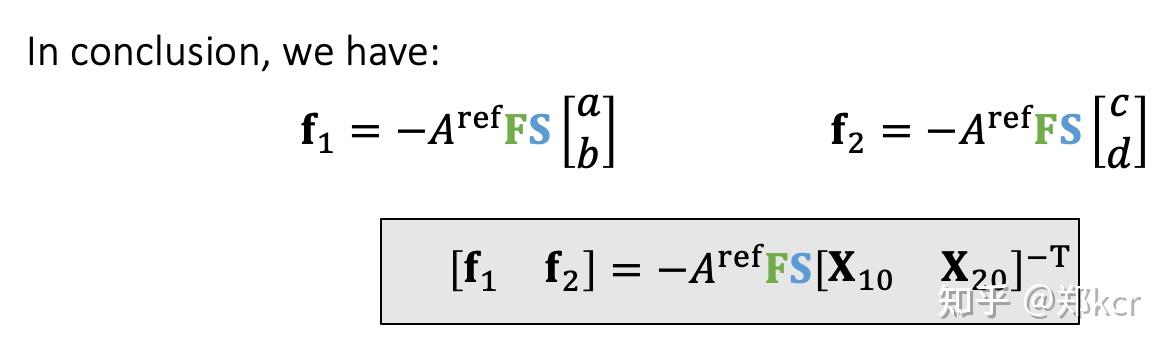
第三个顶点的力 f_3 = - f_1 - f_2
这个也好理解,本质上FEM就类比一个二维的弹簧,原本弹簧两个端点收到的力相加为零。因为这些力是弹簧内部的物质张力施加在端点上的。
二维或者三维的FEM
首先定义能量,接着计算一下的量

Finite Volume Method (FVM)
Traction与Stress之间的关系
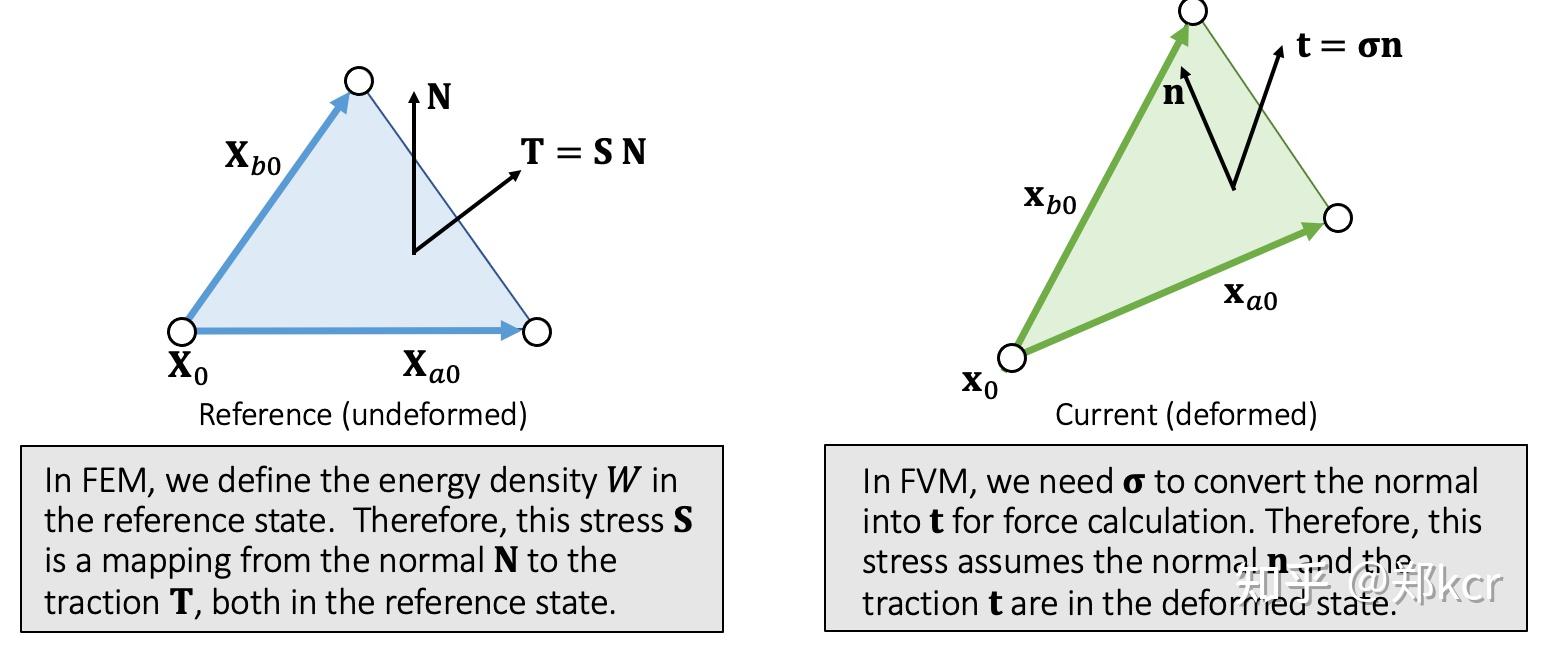
产生形变以后边界的力,等于能量关于形变求二阶导(Stress tensor)乘上边界上的normal。
Stress tensor就是连结 力 与 normal的桥梁。
力/normal的方向可以是相对于形变前定义,也可以是形变后的。无论是形变前还是形变后,只差一个线性变换。
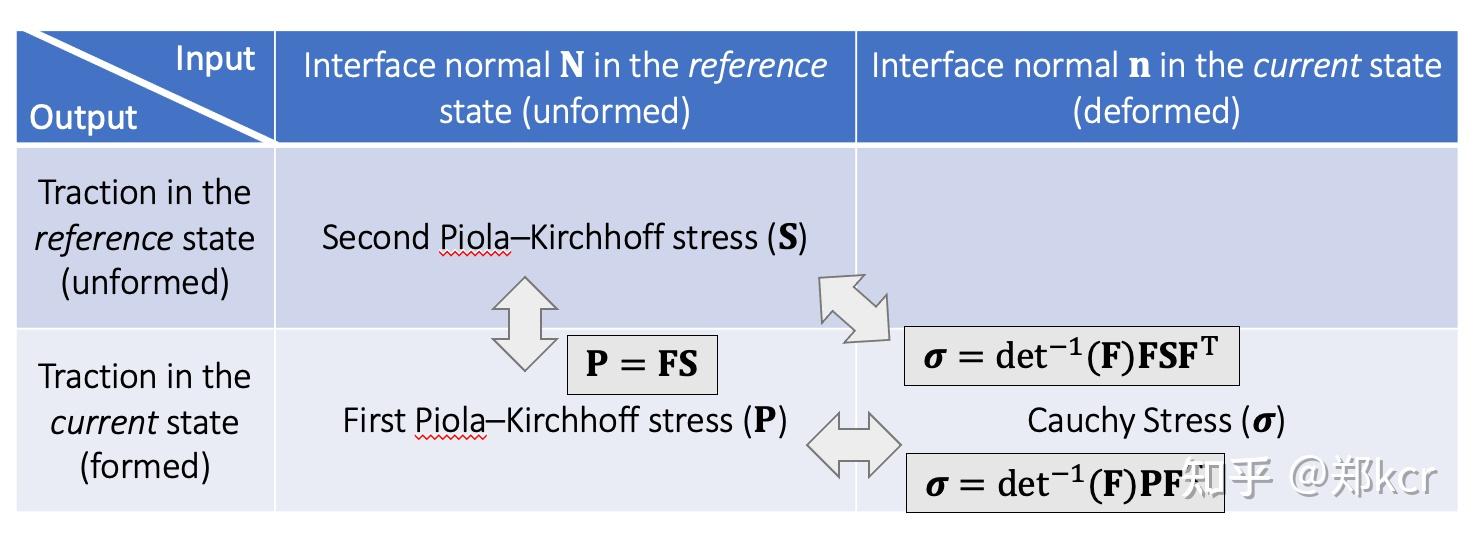
我们还是使用StVK能量,然后和FEM一样计算出Second PK stress。计算得到Cauchy Stress。所以本质上对于linear情形FEM和FVM只是不同的形式,能量一样这样物理模型是一样的。
FVM作用在顶点上的力
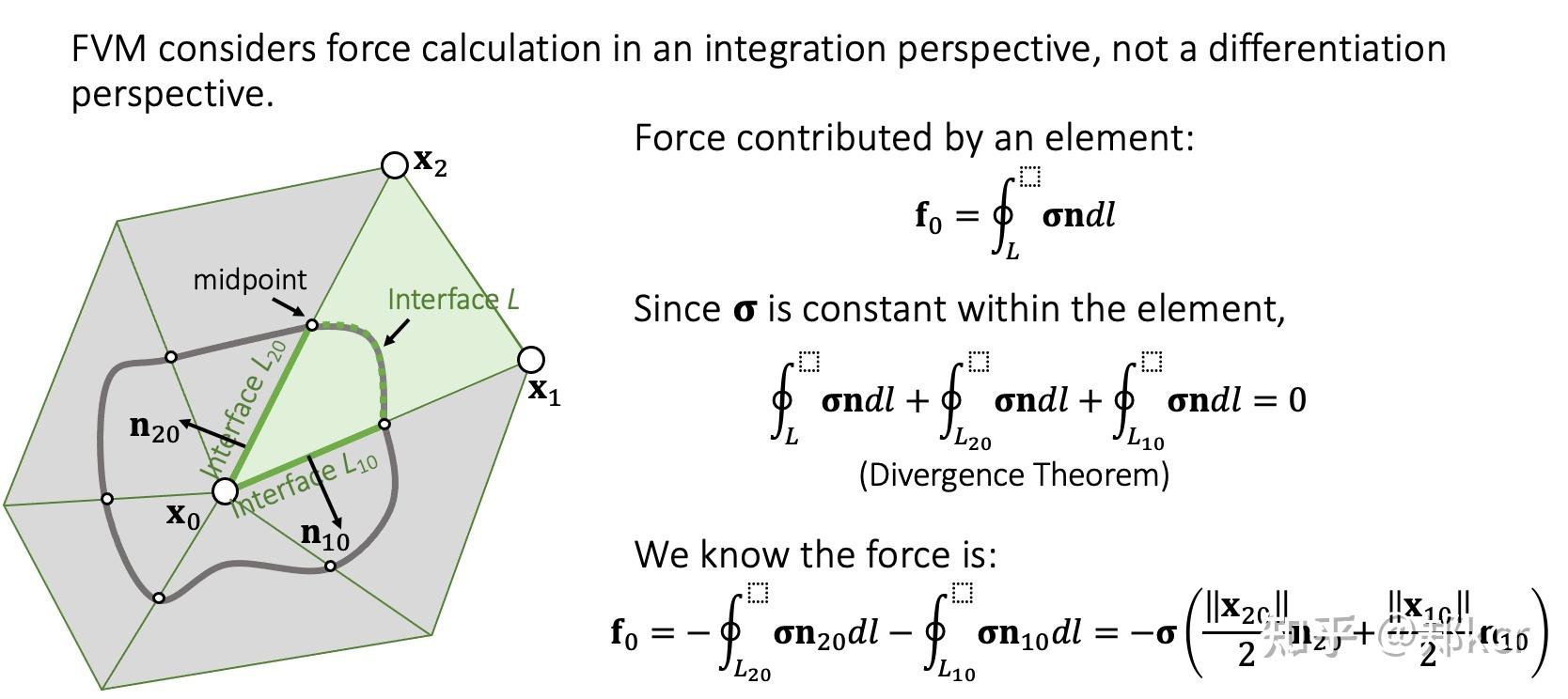
类比一根弹簧,弹簧左侧端点受的力近似为弹簧左半边的所有弹性体施加在端点上的合力。对于二维/三维物体,可以近似的认为是连接两个中点以后小三角形作用在端点上的力。
根据divergenc theorem可以得到一个简单的形式。得到力和Stress的关系。这个就是FVM的全部内容了。
最终得到
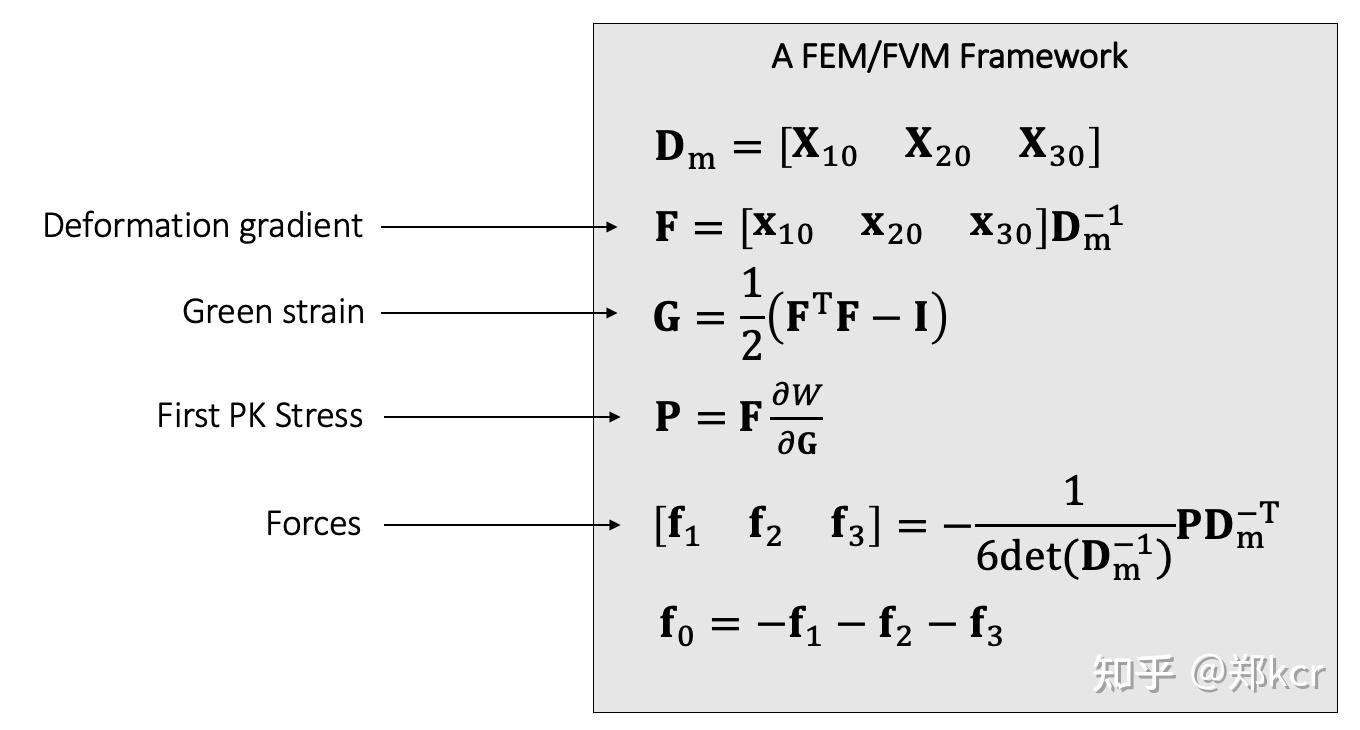
Hyperelastic Models
Isotropic Materials的stress tensor关于rotation不变。stress tensor是线性变换F的函数。对于Isotropic Materials,它是principle stetches的函数(singular values)

再定义SvTK能量
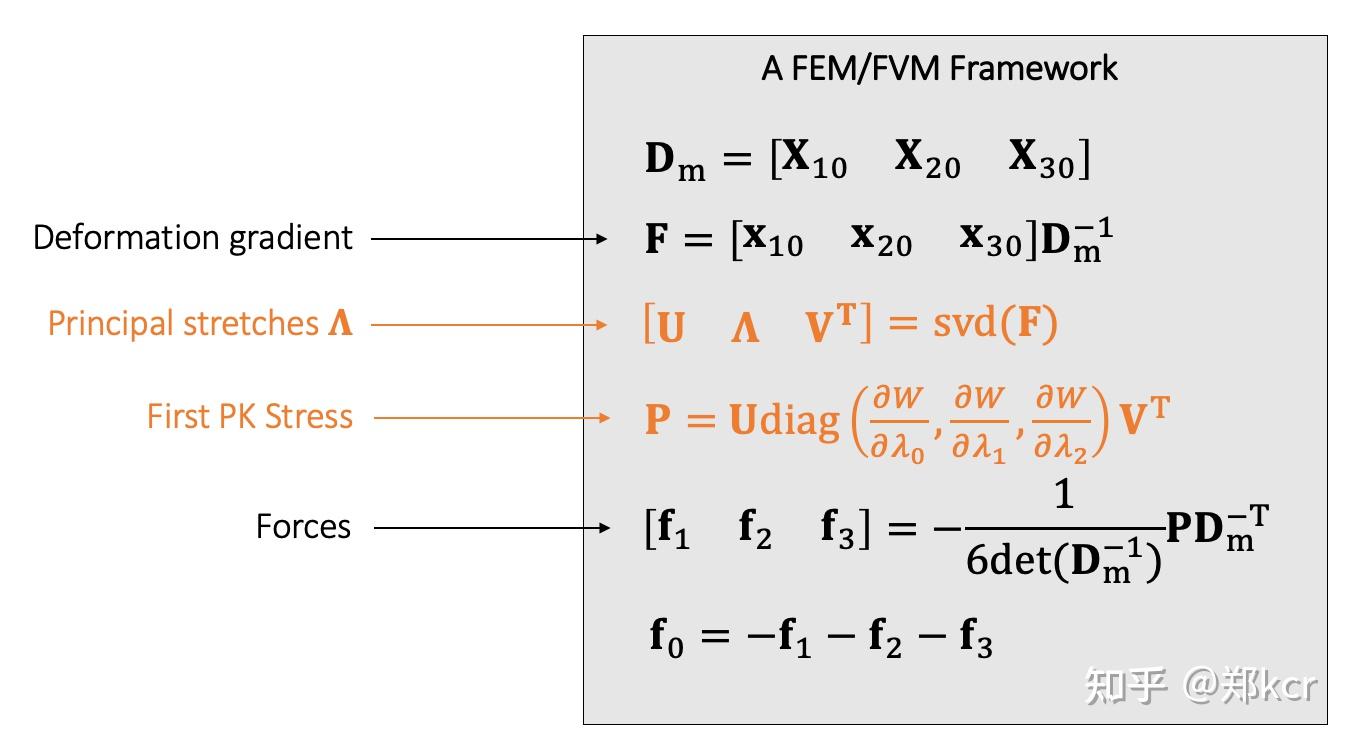
有限元不同的能量形式
SvTK的缺点如下图所示,当比原长还小以后再压缩到某一点能量反而减少。并且移动到负数以后,无法返回正数位置。考虑一个蹦床,当弹到底下以后就反弹不回来。所以不是很好的模型。
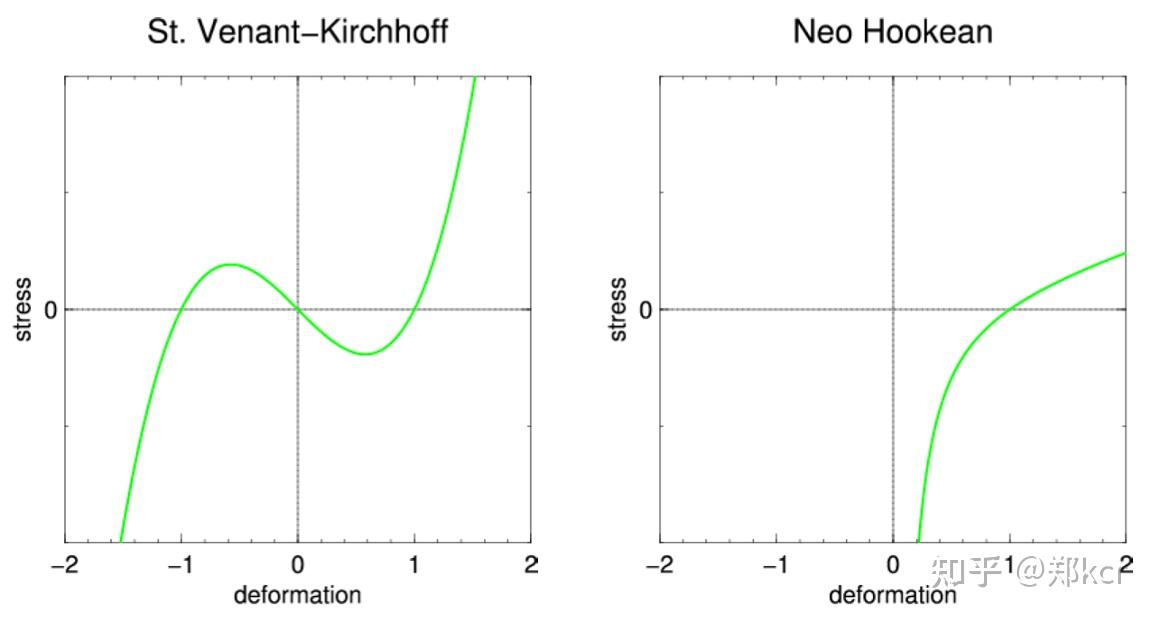
还存在很多种其他的模型。
流体模拟(Shallow wave)
浅水波方程
本质是纯微分方程模拟浅水波。
水波看成是height field,每个点有一个高度。高度h(x)满足的方程,本质就是不可压缩流体的方程。
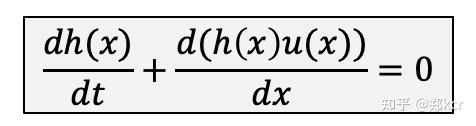
速度u(x)满足的方程
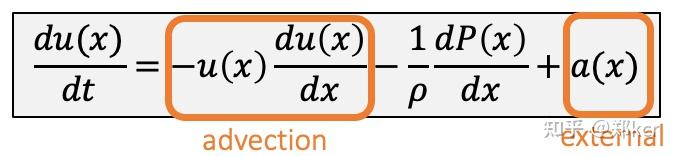
忽略掉外力和advection得到方程。advection项本质上是由于水分子运动到下一个位置,会把它所携带的速度带过来。可以看出当du/dx很大的时候,前一个位置的水的速度相对于当前位置就速度更慢,所以下一时刻水的速度会减少。外力项比如外界有个螺旋桨,就会有外力。
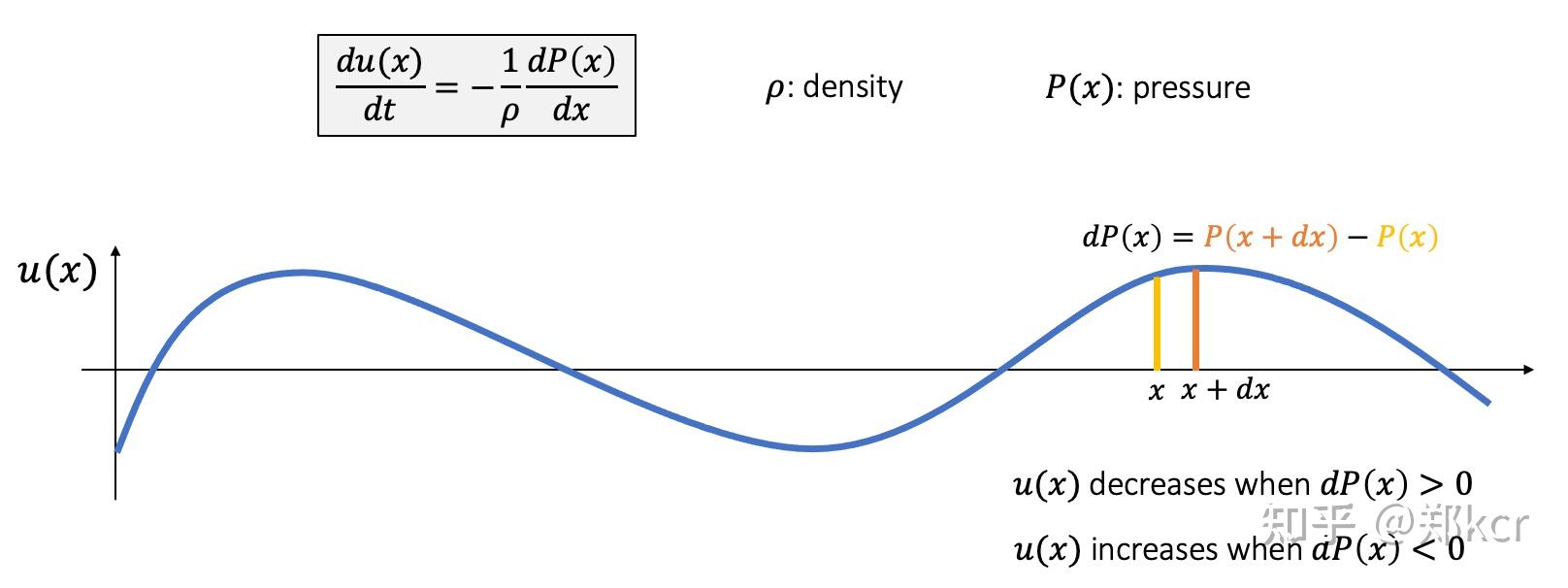
流体的流速变化正比于,压强给水柱的压力。化简得到 浅水波方程Shallow wave equation
直接使用Finite differencing求解就行了。
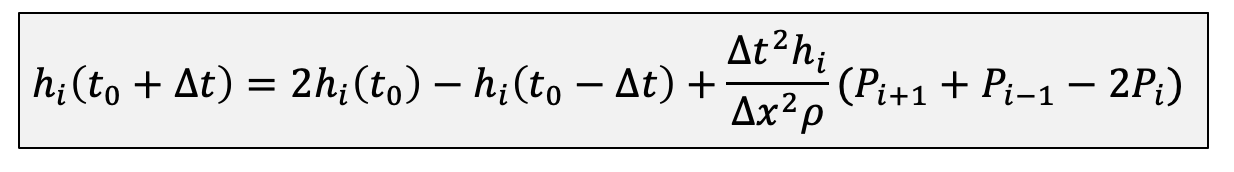
Volume Preservation
需要对迭代公式进行修改,使得流体的体积不变,否则水会变多变少。
比如其中方法之一
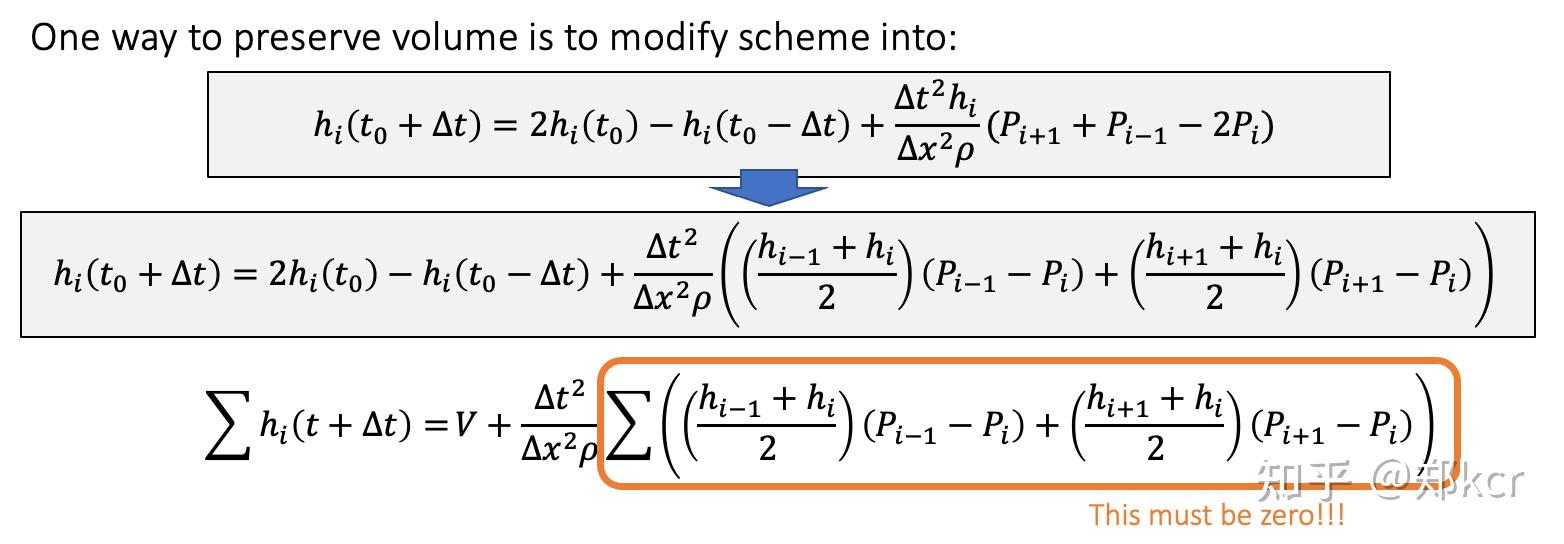
压强
压强正比于深度

黏滞力(能量损失)

边界条件

Dirichlet要求边界的数值固定,类比大海,开放边界。
Neumann boundary要求边界和倒数第二格高度相等,相当于不交换,类比墙,闭边界。
算法

还挺简单的,构建一个网格。然后每个格子的状态就是高度,然后通过浅水波方程不断更新就行了
与刚体交互
假设当前水面是平的。然后我们知道刚体的进入水中的位置。刚体会排开水
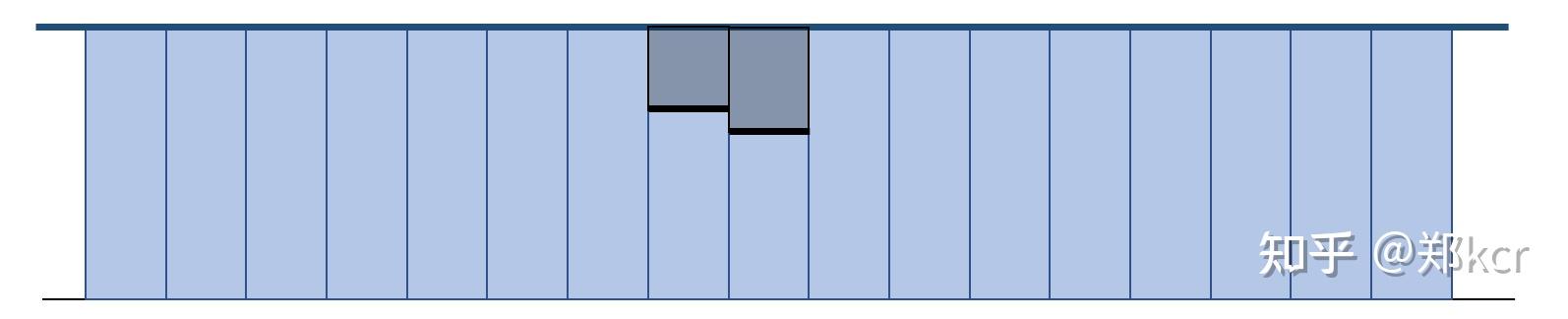
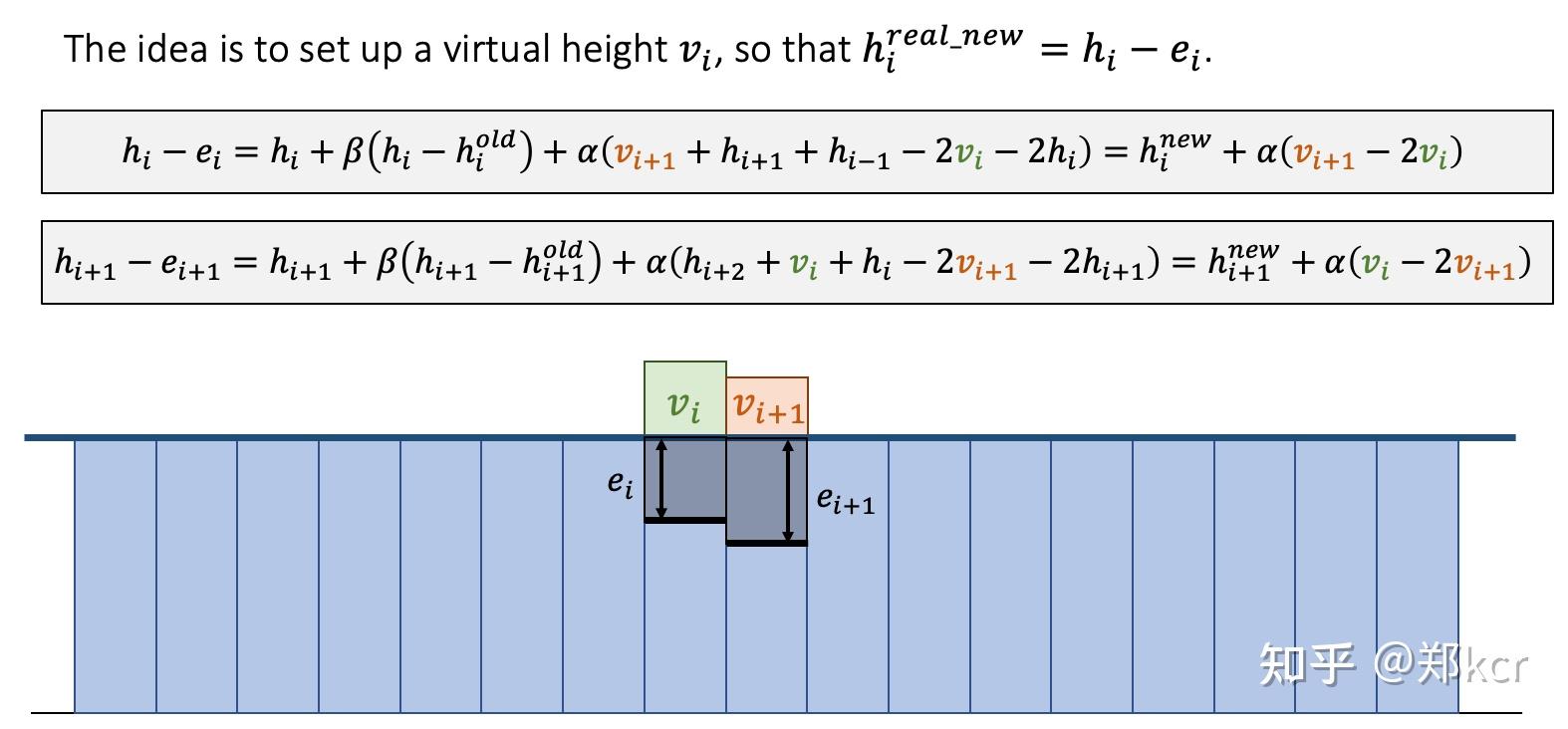
在模拟的时候,我们假设当前步有一个虚拟的水柱。虚拟水柱的长度通过方程组解出:使得下一步更新后的高度满足排开水后的高度。
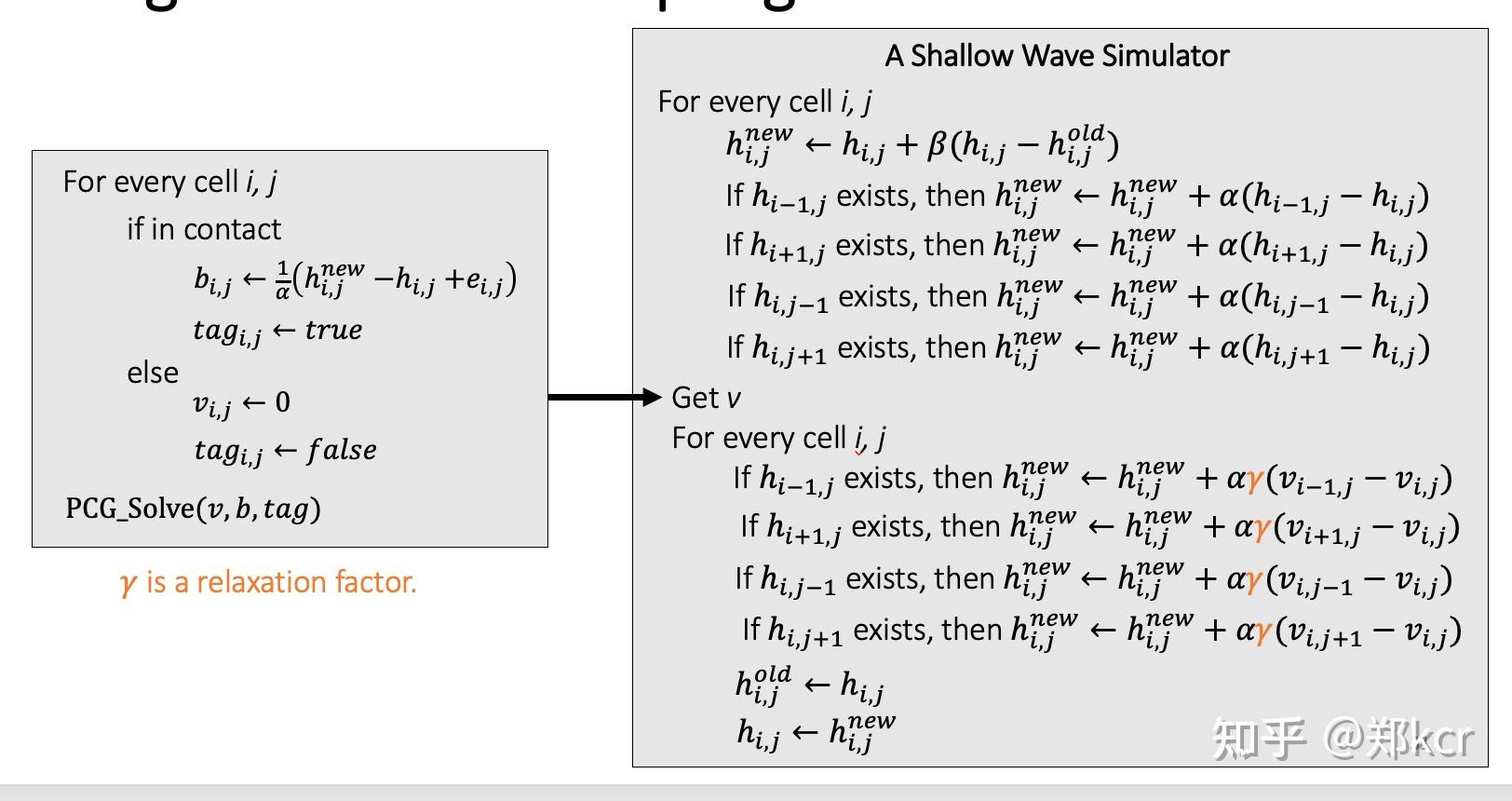
算法
刚体位置的更新,可以使用排开水的体积作为浮力更新刚体的位置
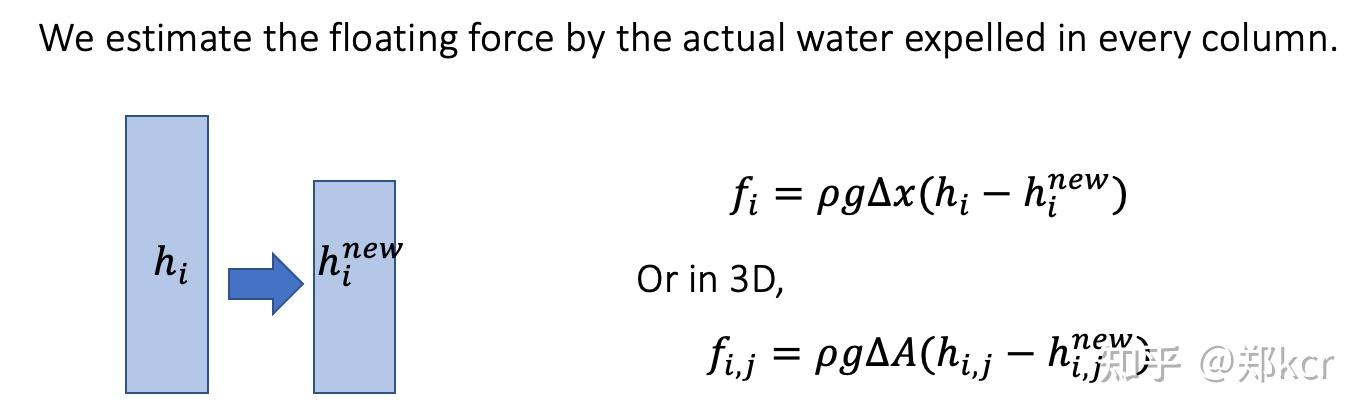
流体模拟(欧拉法、网格法)
本质上是模拟Incompressible, Viscous Navier-Stokes Equations
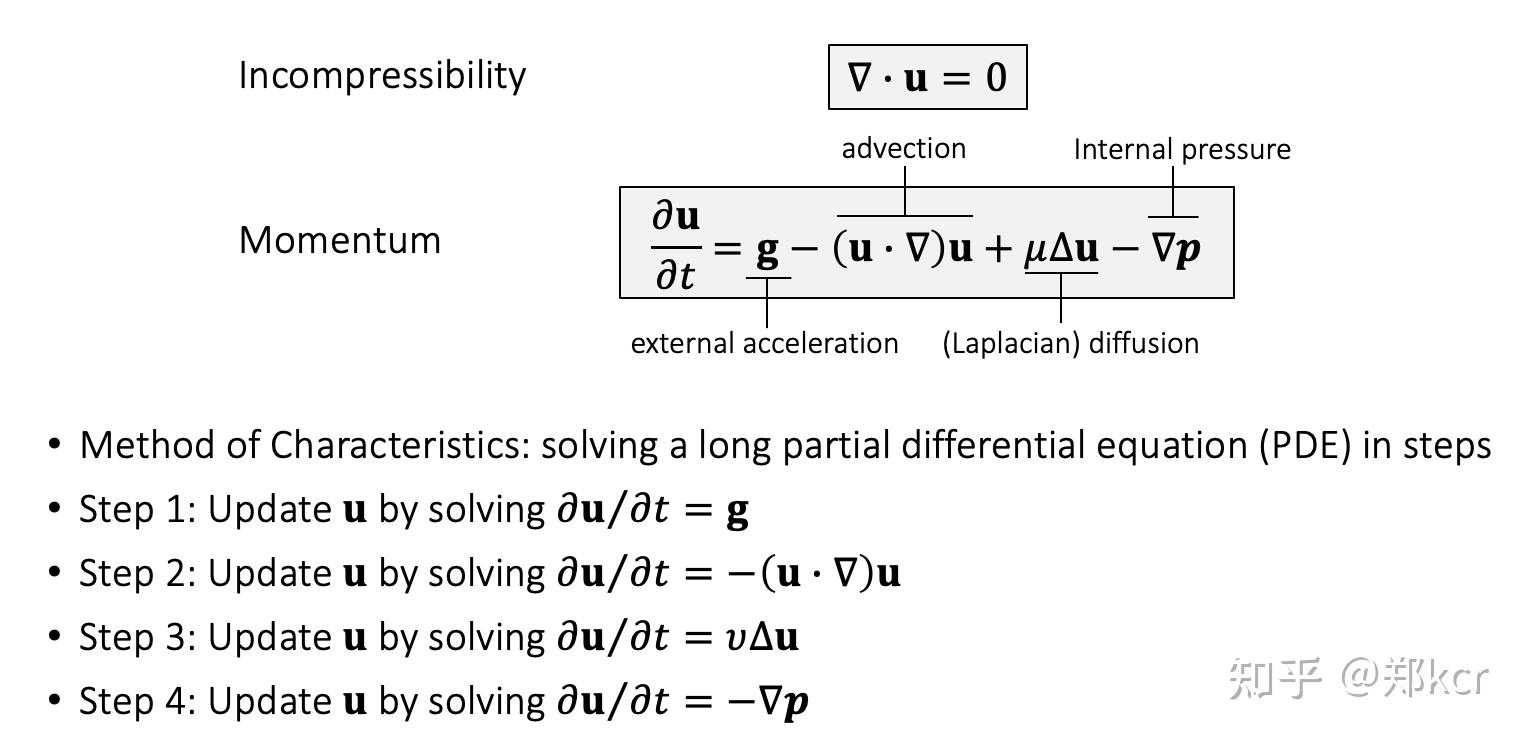
三项压强、外力、advection、diffusion(Laplacian)
使用Method of characteristics依次更新
Staggered Grid
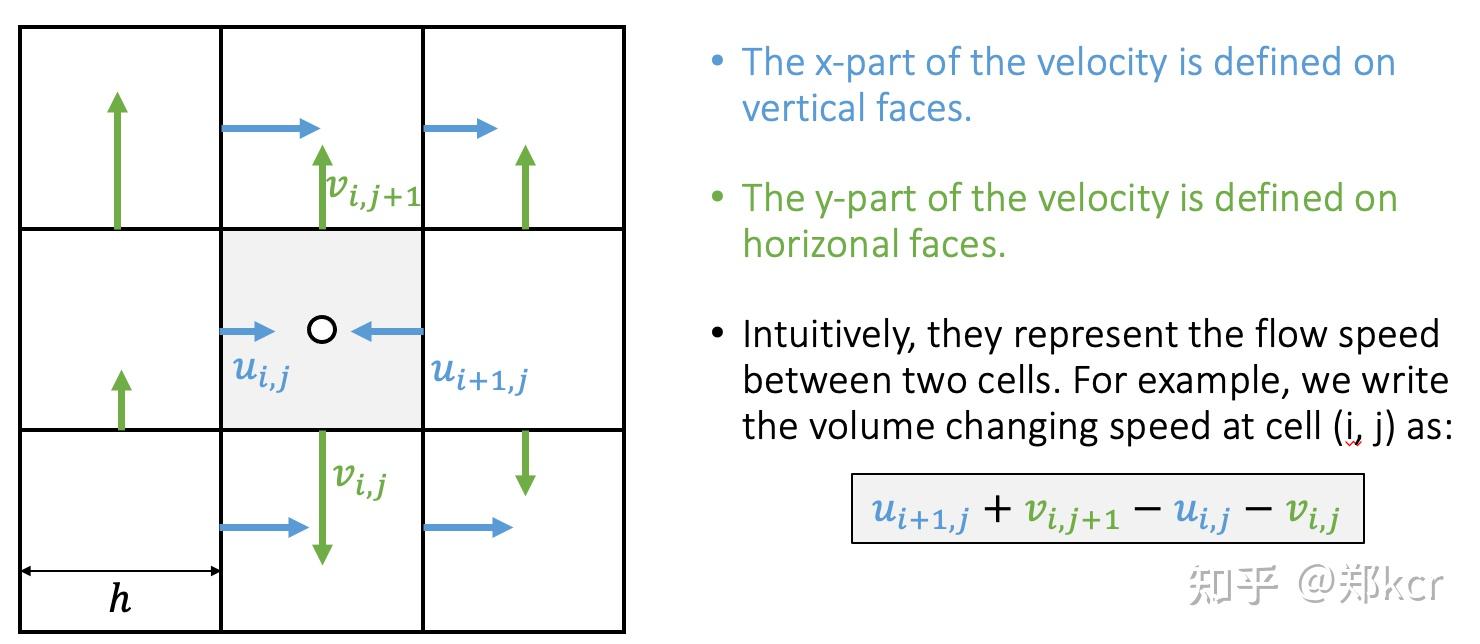
把位置密度等物理量定义在网格中心。一阶导数比如速度定义在网格边界。(一阶导数用Central differencing只能得到网格边界的值,所以定义在网格边界比较方便)
- Step1 : External Acceleration
使用Semi-Lagrangian Method,本质上advection来自于上一时刻的位置把速度带到当前位置
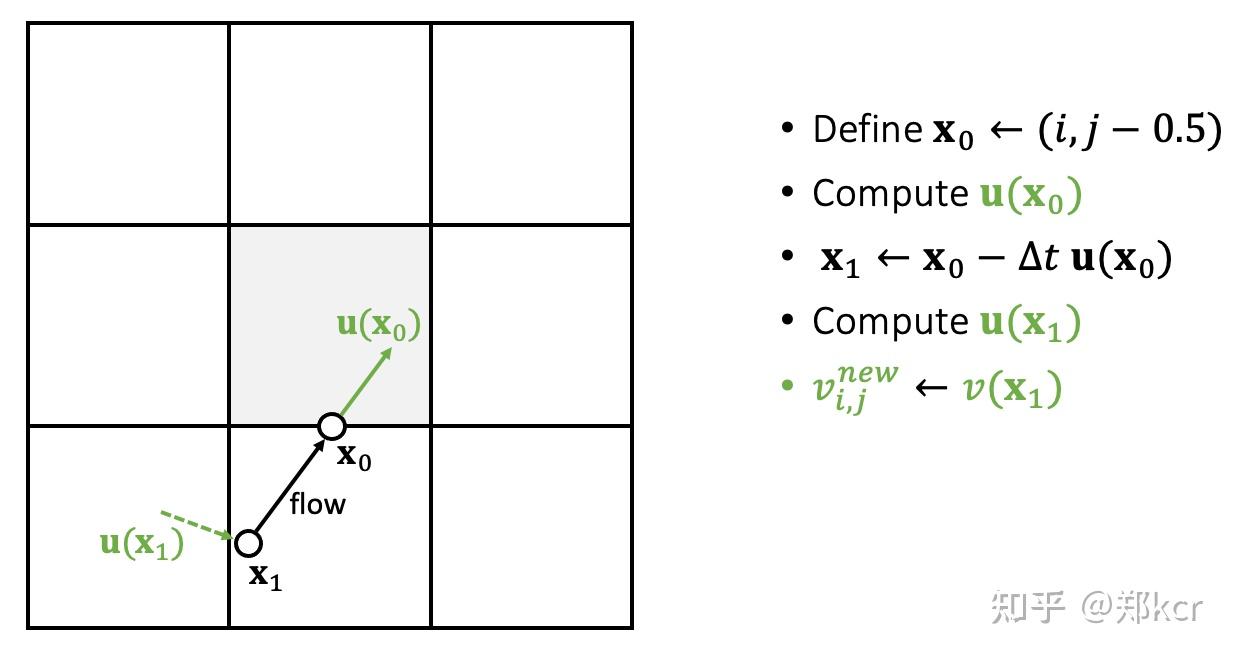
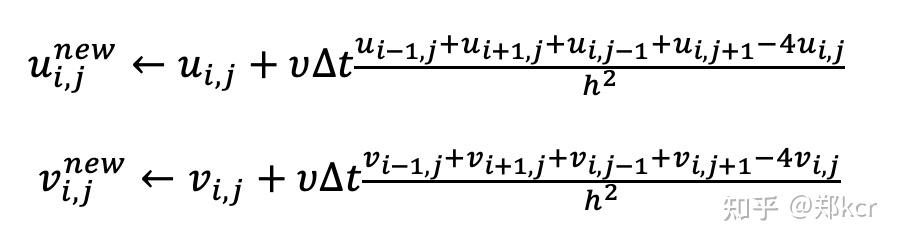
- Step 3: Pressure Projection
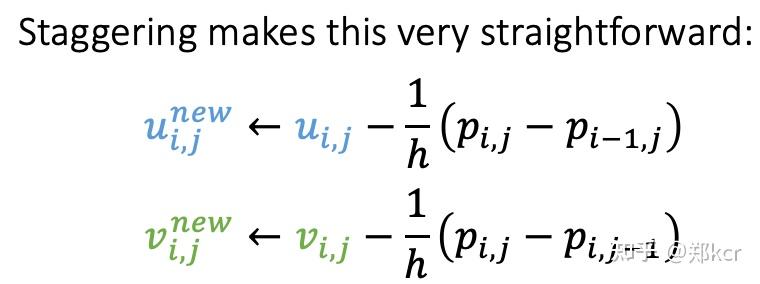
还需要计算pressure,pressure是由于不可压缩导致的,所以我们要求新的速度满足不可压缩条件
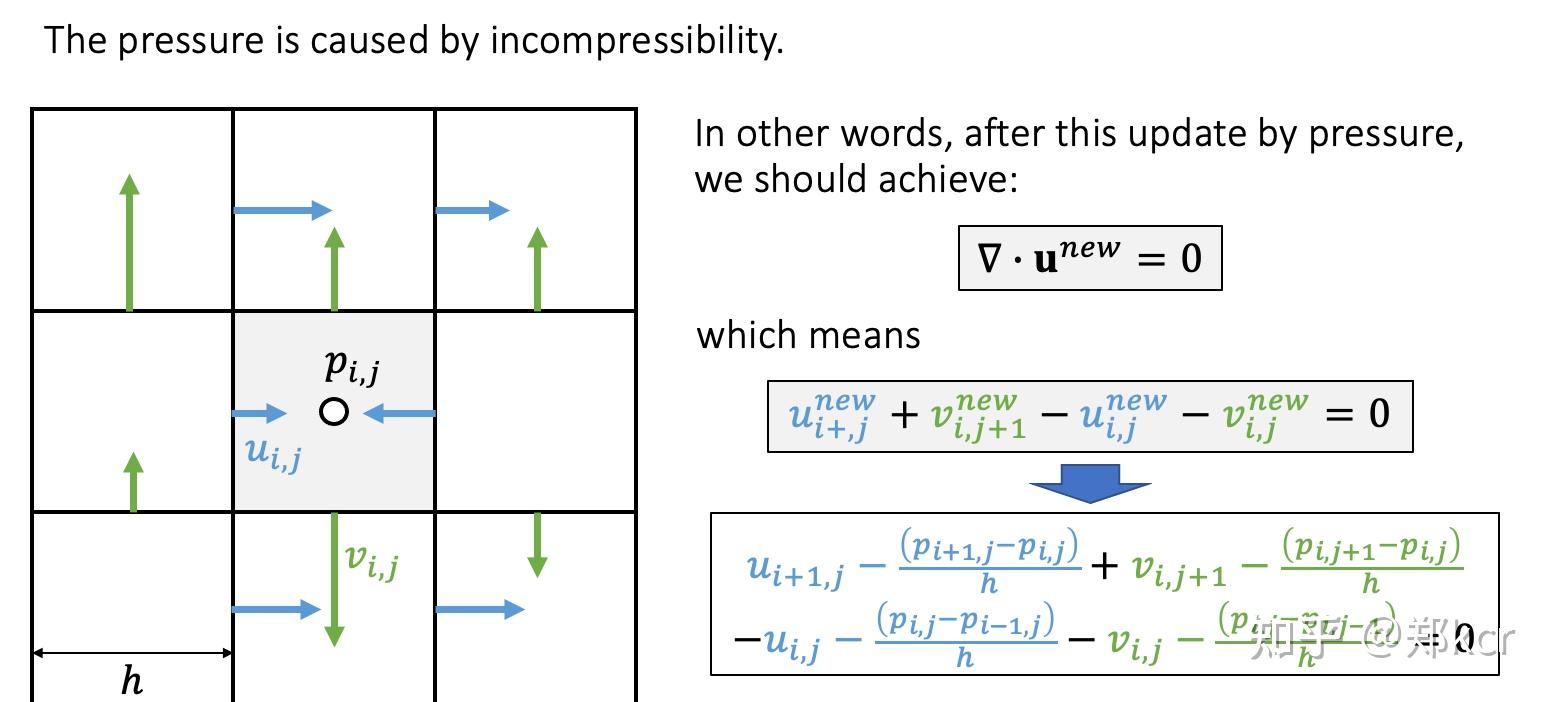
可以通过这些公式计算得到所有的pressure
Air and Smoke
Air simulation与上面的方法类似。
水和空气的界面是一个难点。
总结

模拟完以后还需要用比如Marching cube从网格生成mesh。
流体模拟(拉格朗日法,粒子法)
一般方法
本质上还是流体力学方程。
用一堆粒子模拟流体,每个质点有位置、速度、质量、温度、压强。。。
质点受到的力是重力、压强、Viscosity(黏滞力)
然后使用隐式积分或者显示积分就行了
核心难题在于流体压强和黏滞力如何计算?
Smoothed Particle Hydrodynamics(SPH model)
给定一堆粒子,粒子j携带物理量A_j。我们想要计算某些物理量在空间中的gradient。但是物理量在空间是离散分布的。那么就需要把这些物理量在空间中的某种平均函数得到。
核心问题:如何估计某个新位置x_i处的物理量A_i?(x_i处可能没有粒子)
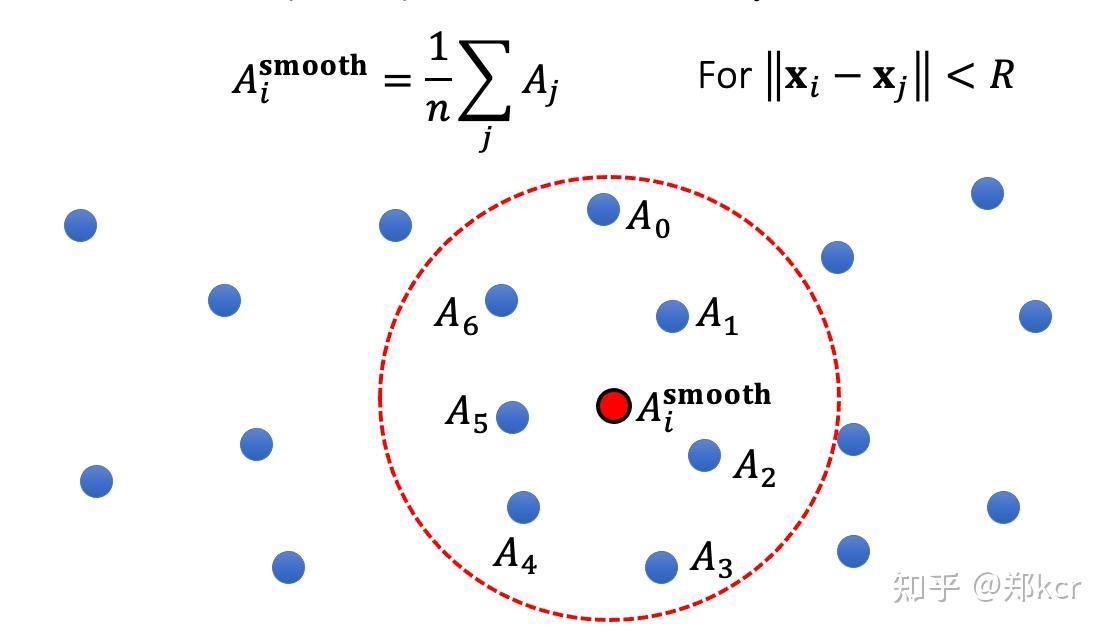
最简单的方法是使用k-nearest Neighbor算法。
升级版的方法,平均的时候把体积和 距离的某个函数(smoothed kernel)作为权重。
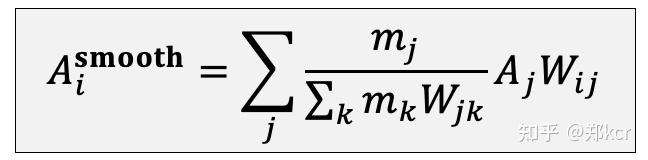
第一项近似代表第j个粒子占的体积。W_ij代表j和i的距离。
W_ij的形式很多种,比如
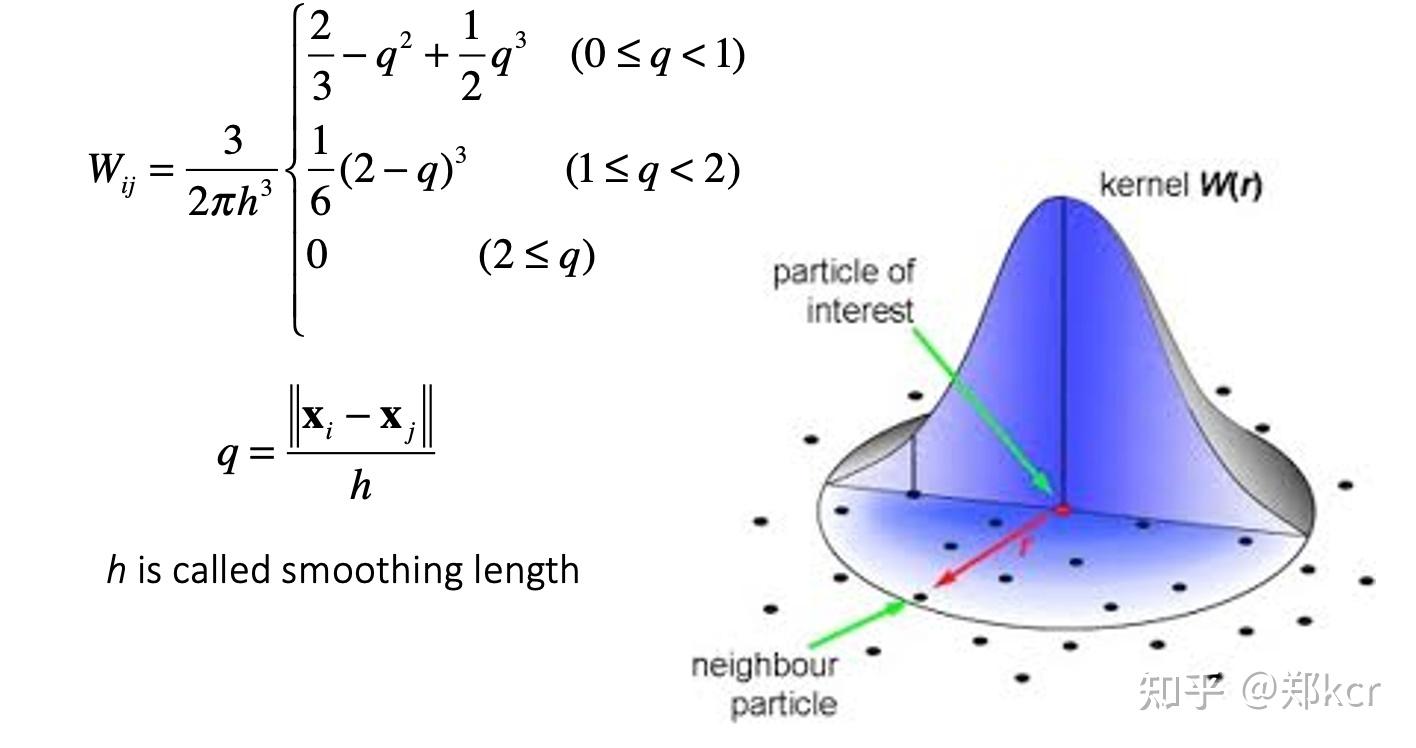
有了这个表达式,就可以计算出物理量在空间中的导数。
SPH流体模拟

重力就是 \mathbf{F}_{i}^{\text {gravity }}=m_{i} \mathbf{g}
压强Pressure:
\rho_{i}=\sum_{j} m_{j} W_{i j}
P_{i}=k\left(\left(\frac{\rho_{i}}{\rho_{\text {constant }}}\right)^{7}-1\right)
水的压力大概是Gadient of Pressure:
\mathbf{F}_{i}^{\text {pressure }}=-V_{i} \nabla_{i} P^{\text {smooth }}
P_{i}^{s m o o t h}=\sum_{j} V_{j} P_{j} W_{i j}
Viscosity Force:
\mathbf{F}_{i}^{v i s \cos i t y}=-V m_{i} \Delta_{i} \mathbf{V}^{\text {smooth }}
\mathbf{v}_{i}^{\text {smooth }}=\sum_{j} V_{j} \mathbf{v}_{j} W_{i j}
以上的公式都可以严格的通过流体力学方程推导出来。
Nearest Neighbor Search
上述算法中,速度最慢的反而是寻找粒子的Nearest neighbor。
可以使用Spatial Partition方法来做。比如Octree, KD-Tree, Binary Spatial Partitioning Tree
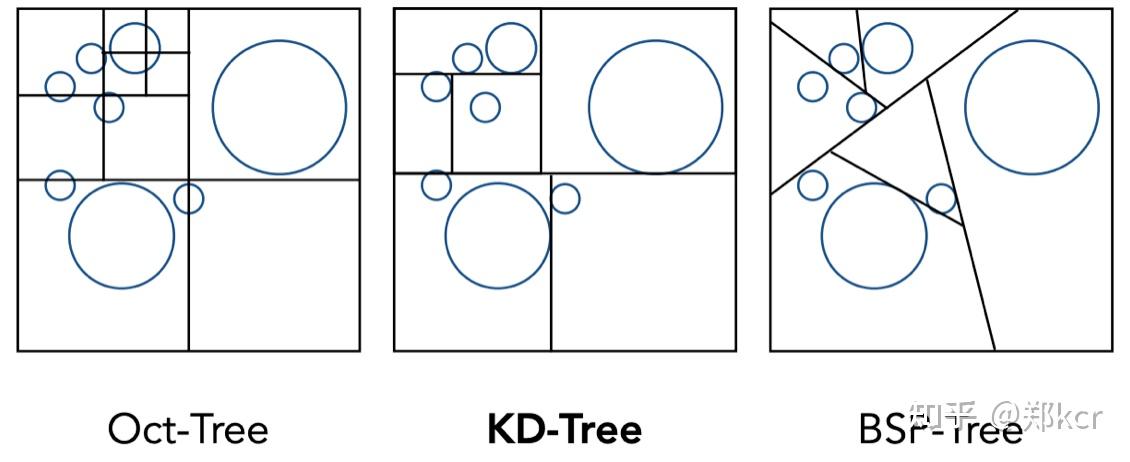
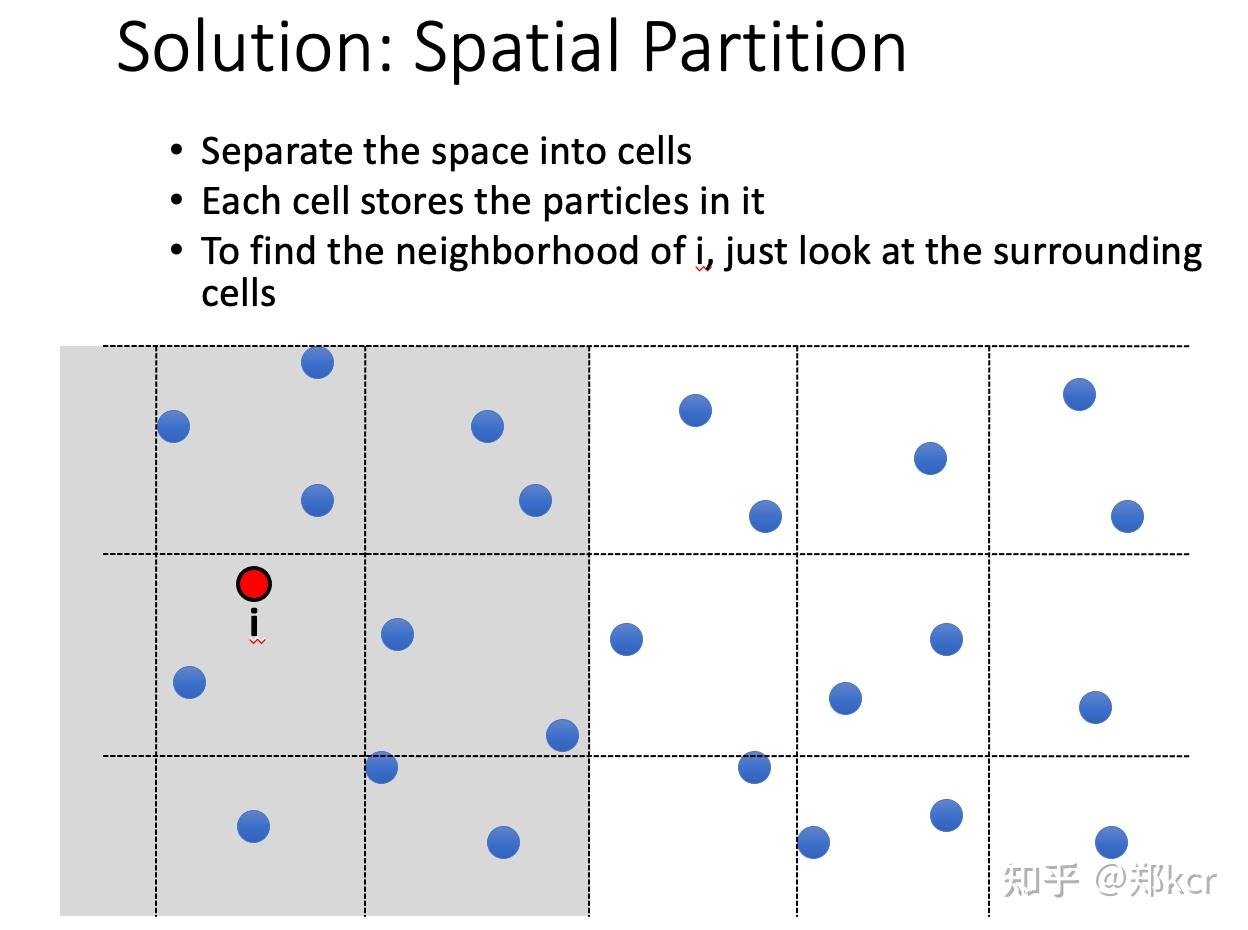
Fluid Display
需要从来粒子中还原出水面。简单的算法比如把粒子都变成球面,然后求并集再平滑化得到水面。
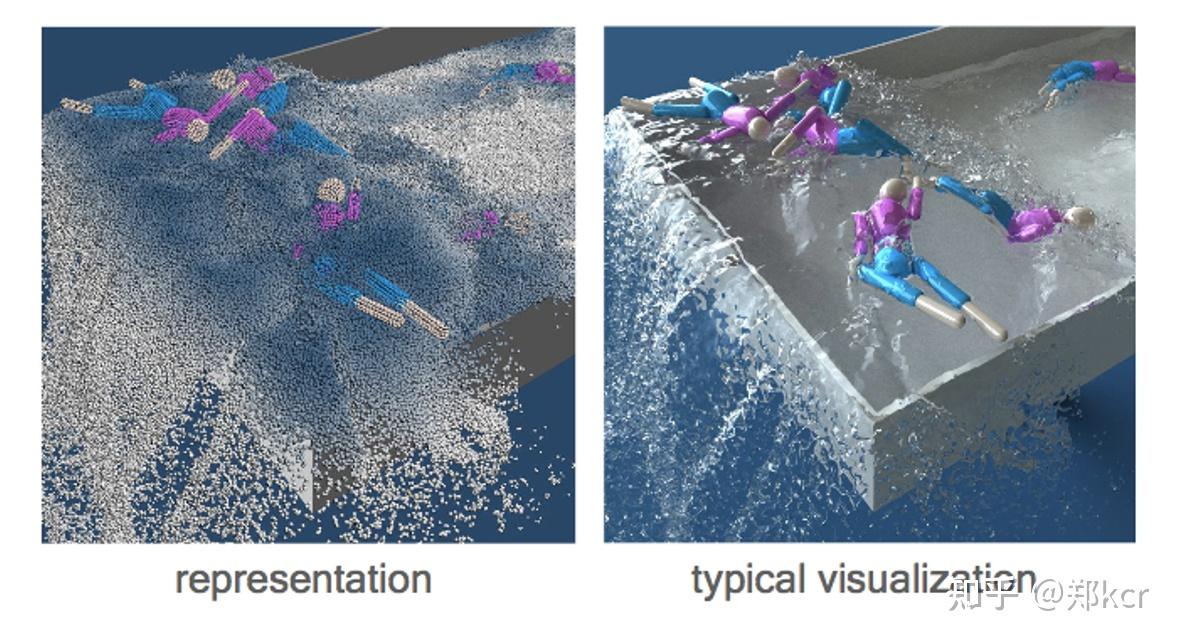 |
本帖子中包含更多资源
您需要 登录 才可以下载或查看,没有账号?立即注册
×
|