黑盒优化：超参数优化算法最新进展总结

APSchmidt · 发表于 2022-4-15 11:40

本文是超参数系列文章的汇总：
张大快：超参数优化(一): 简介
张大快：超参数优化(二): 贝叶斯优化
张大快：超参数优化(三): 实验设计
张大快：超参数优化(四): TuRBO--基于信赖域的贝叶斯优化
张大快：超参数优化(五): MCTS+TuRBO-基于蒙特卡洛树搜索的贝叶斯优化
张大快：超参数优化(六): HEBO-基于异质方差进化的贝叶斯优化
张大快：超参数优化(七): pySOT和POAP-代理模型优化工具箱及其异步并行框架
<hr/> 欢迎关注: simplex101 ,了解更多超参数优化（黑盒优化）分享内容。
<hr/>一、简介

黑盒优化在工业设计中有着广泛的应用，机器学习中的超参数优化是黑盒优化的一种。近年来，随着深度学习的不断发展，深度学习建模中涉及到的超参数数量远超传统机器学习方法（如XGBoost、SVM等)。机器学习中的超参数优化，特别是深度学习，越来越凸显重要作用，引起了学术界和工业界的重视：

2021年，QQ浏览器在国际综合AI学术会议之一顶会CIKM和中国计算机学会（CCF）多媒体技术专委会支持下举办2021AI算法大赛。自动超参数优化赛题为超参数优化问题或黑盒优化问题：给定超参数的取值空间，每一轮可以获取一组超参数对应的Reward，要求超参数优化算法在限定的迭代轮次内找到Reward尽可能大的一组超参数，最终按照找到的最大Reward来计算排名。[1]
2020年，在2020 NeurIPS 举办了黑盒优化的比赛 [2]，比赛任务是对机器学习中的超参数进行优化。

在有限的参数搜索限制条件，寻找能够使机器学习模型达到一个较优的解(或者Loss)，是一个很具挑战的黑盒优化问题：

$\begin{aligned} \max_{x\in X} f(x) \end{aligned} \tag{1}$
其中为参数空间，为我们需要最优化的黑盒函数。
2021年QQ浏览器动超参数优化初赛，限制为100个评估点，时间不超过600s，则问题可以建模为：

$\begin{aligned} \max_{x\in D} \enspace &f(x)\\ \text{ } D&=\{x_1,x_2,...,x_{100} \}, x_i \in X \\ & \sum_{i=1}^{20} time(i) <= 600s \end{aligned} \tag{2}$
本文作者参与了2021年QQ浏览器动超参数优化比赛，参赛过程中调研了2020 NeurIPS BBO的参赛方案及当前业界最新超参数优化和黑箱优化的技术进展，在业余时间进行了相应的总结，形成此系列文章，希望对超参数优化和黑盒优化感兴趣的同学能有所启发。
本文的组织形式如下：

第2章：介绍贝叶斯优化框架，包括代理模型、采集函数等；
第3章：介绍实验设计的内容，侧重介绍Halton序列、拉丁超立方序列和Sobol序列的生成 [13] [14]；
第4章：介绍基于信赖域的贝叶斯优化方法TuRBO [7]；
第5章：介绍基于蒙特卡洛树搜索的贝叶斯优化方法(MCTS+TuRBO) [5] [6] ；
第6章：介绍基于异质方差进化贝叶斯优化方法（HEBO）[3] ；
第7章：介绍基于pySOT和POAP的代理模型优化工具箱及其异步并行框架[8] ；
第8章：介绍在QQ浏览器2021超参数优化大赛参赛经验总结；
第9章：总结和展望。

注：本系列相关章节的部分内容后续更新可能会有调整。
二、贝叶斯优化

摘要：近年来贝叶斯优化在求解黑盒函数问题中应用越来越广泛，已经成为超参数优化的主流方法。贝叶斯优化是一种全局优化的方法，目标函数只需要满足一致连续或者利普希茨连续等局部平滑性假设；通过引入采集函数，进行有效探索和利用，能在较少的评估次数下取得复杂目标函数的近似解。
2.1 背景

自动超参数优化是黑盒优化的一个具体应用。黑盒优化具有如下的特点：

优化目标：没有显式的函数表达式，获取不到其梯度信息；其值域分布通常是多峰、非凸非凹的复杂昂贵函数；
函数空间：由连续、离散整数值构成的，且实际应用中维度较高；
优化目标求解：求解非常昂贵耗时，在工业设计中通常一次评估花费数十万至百万元以上；在大规模的深度学习训练中通常花费若干天甚至数周时间进行一次参数搜索。

黑盒优化的求解方法：

元启发式算法(meta-heuristic algorithm) [17]：遗传算法 (genetic algorithm, GA)、差分进化(differential evolution, DE) 算法、粒子群算法 (particle swarm optimization, PSO)、进化策略(evolutionary strategies, ES)
无导数优化方法[18] ：随机搜索、直接搜索法；基于模型的如多项式方法，径向基函数插值方法和基于代理模型方法，如贝叶斯优化。

近年来，贝叶斯优化在求解黑盒函数问题中应用越来越广泛，已经成为超参数优化的主流方法。贝叶斯优化的优势[15] ：

是一种全局优化的方法，目标函数只需要满足一致连续或者利普希茨(Lipschitz)连续等局部平滑性假设；
能在较少的评估次数下，取得复杂目标函数的近似解；
引入采集函数，进行有效的探索和利用(Exploration and Exploitation)

我们将在本节末尾讨论贝叶斯优化的局限性。
2.2 贝叶斯优化建模

2.2.1 问题定义

超参数优化问题定义：

$\begin{aligned} \arg min_{x\in X} \enspace f(x) \end{aligned} \tag{3}$
其中，为超参数的一组设置取值，为混合设计空间(Design Space)。为超参数优化中，我们需要优化的目标（如最小化Loss)。
超参数优化算法的目标是以最快的方式找到全局最优解$x^ = \arg max_{x\in X} f(x) $。*
为了达到这个目标，贝叶斯算法求解超参数优化问题，通常分为两步：

第1步：学习一个代理模型(Surrogate Model)；
第2步：通过采集函数(Acquisition Function)，来决定输出下一个采集点。

2.2.2 贝叶斯优化框架

由贝叶斯定理：

$\begin{aligned} 后验分布 &= 先验分布 + 观察数据\\ p(A|B) &= \frac{p(B|A) \cdot p(A)}{ p(B)} \end{aligned} \tag{4}$

$p(A)$ 为先验分布，即我们的代理模型；
$p(B|A)$ 为给定代理模型，观察数据的分布；
$p(A|B)$ 为后验分布，即给定观察数据之后代理模型新分布。

贝叶斯优化框架：

图2.1：贝叶斯优化框架

步骤1：随机初始化点 $X_{init} = \{x_0,x_1,...,x_{n_0-1}\}$
步骤2：获得其对应的函数值 $f(X_{init})$ ，初始点集 $D_0=\{X_{init} ,f(X_{init})\}$
令, ，循环直到达到最大次数
- 步骤3：根据当前获得的点集 $D_{t-1}$ ，构建代理模型
- 步骤4：基于代理模型，最大化采集函数 $\alpha(x|D_{t-1})$ ，获得下一个评估点:

$x_t= argmin \enspace \alpha(x|D_{t-1}) \\$

步骤5：获得评估点 $x_t$ 的函数值 $f(x_t)$ , 将其加入到当前评估点集合中:

$D_t=D_{t-1} U \{x_t,f(x_t) \} \\$

步骤6：输出最优候选评估点： $\{x^*,y^*\}$

2.3 代理模型

当黑盒函数的自变量是连续值时，高斯过程回归模型(GPs)是一个非常高效的代理模型。对于黑盒函数，我们通常假设其符合某一个GPs先验分布。高斯过程回归模型(GPs)有如下的两方面来决定[3]：

均值函数；
协方差函数(矩阵)，或者核函数，其中为核函数超参数。

基于上面两点，我们通常假设我们观测到的函数值通过如下的形式产生：

$y_{l} = f(x_l) + \epsilon_{l}， where \enspace \epsilon_{l} \sim N(0,\sigma_{noise}^2 ) \\$
进而，可以得到高斯似然函数形式：

$y_{l}|x_{l} \sim N(f_l ,\sigma_{noise}^2 ) \\$
其中, 服从如下的分布：

$f(x) \sim GP(m(x),k_{\theta}(x,x^{'})) \tag{5}$
通常假设GP kernel 是平稳的，只依赖于两个点和之间的模，进一步我们假设在带噪音分布条件数据点是平稳的且同质的。如果我们观测的数据点不满足这个条件，我们将不能很好的近似黑盒函数。
2.4 采集函数

给定先验和观察数据，由贝叶斯定理我们可以得到相应的后验分布：

$后验分布= 先验分布 + 观察数据 \\$
采集函数是根据后验分布来构造的。在选取GPs作为代理模型条件下，其后验分布仍然是高斯分布：

$p(f(x_{1:q})| D) = N(\mu_{\theta}(x_{1:q}), \sum_{\theta}(x_{1:q})) \tag{6}$
接下来我们列出贝叶斯优化中常见的3种采集函数[3]：

提升的概率 $(Probability improvement ,PI)$ :

$\alpha_{PI}^{\theta} (x_{1:q} | D ) = E_{post.}[\max_{j\in 1:q}\{H\{f(x_j) - f(x^+) \}\}] \tag{7}$
其中为左连续的阶跃函数或开关函数。采集函数PI的原理是在当前的邻域附近，找到比大的候选点，取这些概率最大的点，而不管比大多少。

提升的期望 $(Expected Improvement ,EI)$ :

$\alpha_{EI}^{\theta} (x_{1:q}|D) = E_{post.}[\max_{j\in 1:q}\{ReLU(f(x_j) - f(x^+))\}] \tag{8}$
相比，给出了下一候选点比当前最优值大多少的问题（提升期望)

上置信边界 $(Upper confidence bound ，UCB)$ :

$\alpha_{UBC}^{\theta} (x_{j}) = E_{post.}[\max_{j\in 1:q}\{ \mu_{\theta} (x_j) + \sqrt{\beta \pi /2 } | \gamma_{\theta} (x_j) | \}] \tag{9}$
其中是后续点的后验均值，
不同的采集函数在处理具体问题时有不同的优缺点[15] ：

图2.2：采集函数优缺点对比

和 $UCB$ 都倾向于选取高均值高方差的候选点，但候选点并不趋一致[16] ：

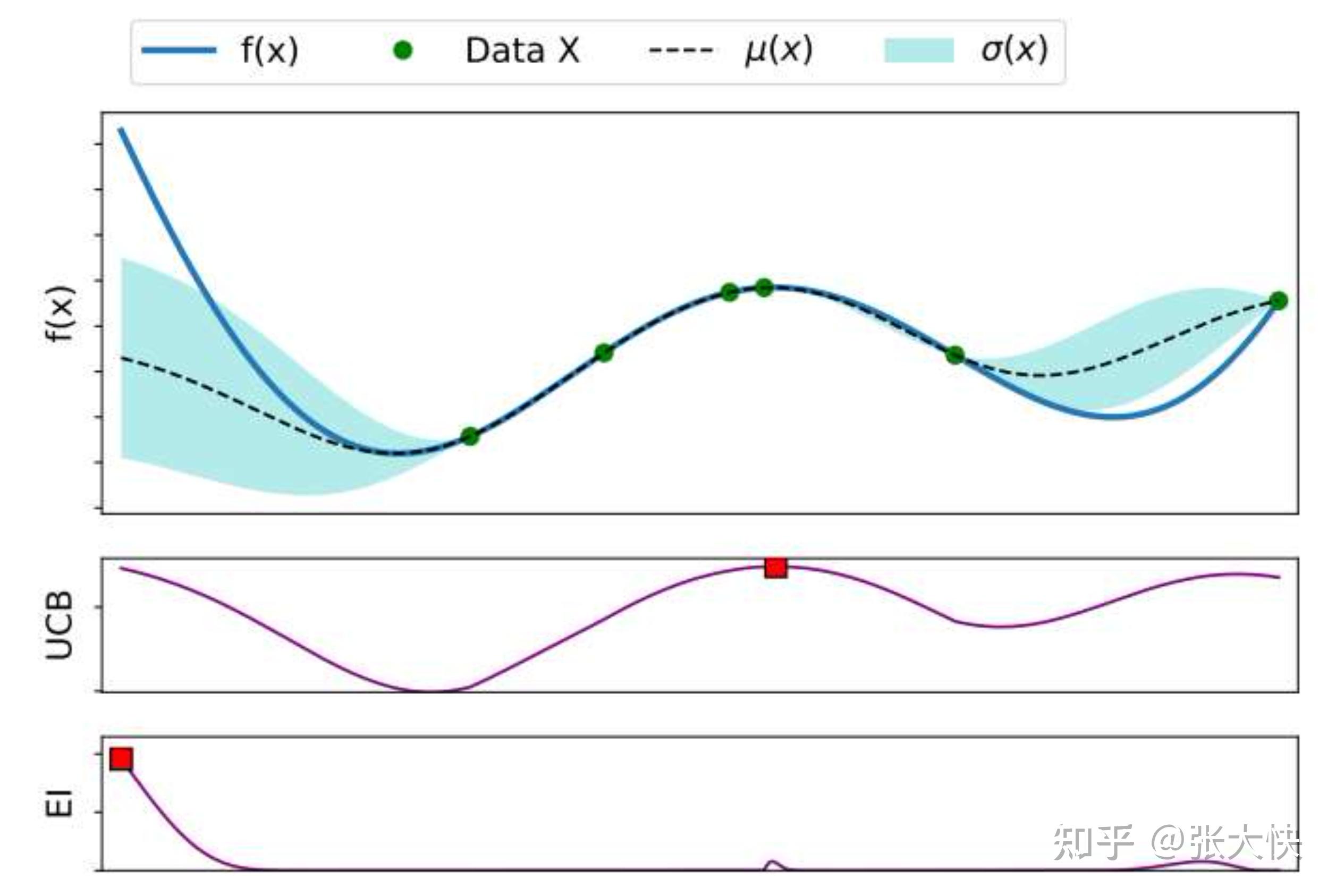
图2.3：EI和UCB不一致情况

2.5 贝叶斯优化进一步探讨

贝叶斯优化中存在的难点：

代理模型：我们通常选取GPs；当我们求解的问题维度变高时，GPs求解的复杂度变高；如何求解高维的贝叶斯优化问题，是一个值得探讨和研究的问题；
采集函数：通常选取上述函数中的一个作为代理模型的采集函数（中途不会更改采集函数）。这个采集函数相对于我们的代理模型和我们要优化的问题是否是最优的呢？我们在HEBO这一节详细讨论这个问题；
和具体优化问题相关：在应用贝叶斯优化求解实际问题，通常要根据实际问题，结合相关的领域知识选择合适的代理模型和采集函数，如我们后续讨论的没有”一招鲜吃遍天“的方法。

三、实验设计

摘要：什么是实验设计？DOE（Design of Experiment）实验设计，实验设计通过对实验进行合理安排，以较小的实验规模和较短的实验周期和较低的实验成本，获得理想的实验结果以及得出科学的结论。本文介绍了实验设计的基本概念、点集偏差、拟随机序列和拉丁超立方生成方法，推荐在实际应用中使用Sobol和拉丁超立方序列[21]。

3.1 实验设计简介

图3.1：现代实验设计发展历程

实验设计在黑盒函数优化、超参数优化中有较广泛的应用。如上图所示，现代实验设计发展起来的方法有如下几种[13]：

静态方法(Static)
- 和实验系统无关(Systerm free)，图中圆圈1
  - 蒙特卡洛、拟蒙特卡洛方法
  - 拉丁超立方方法、最优拉丁超立方方法
- 和实验系统相关(Systerm aided)，图中圆圈2
  - 最大熵、最小均方误差
自适应方法(Adaptive)，图中圆圈3
- MSD-CV方法
- LOLA-Voroni方法

实验设计的分类树如下图所示，感兴趣的读者可以参考论文[13]。

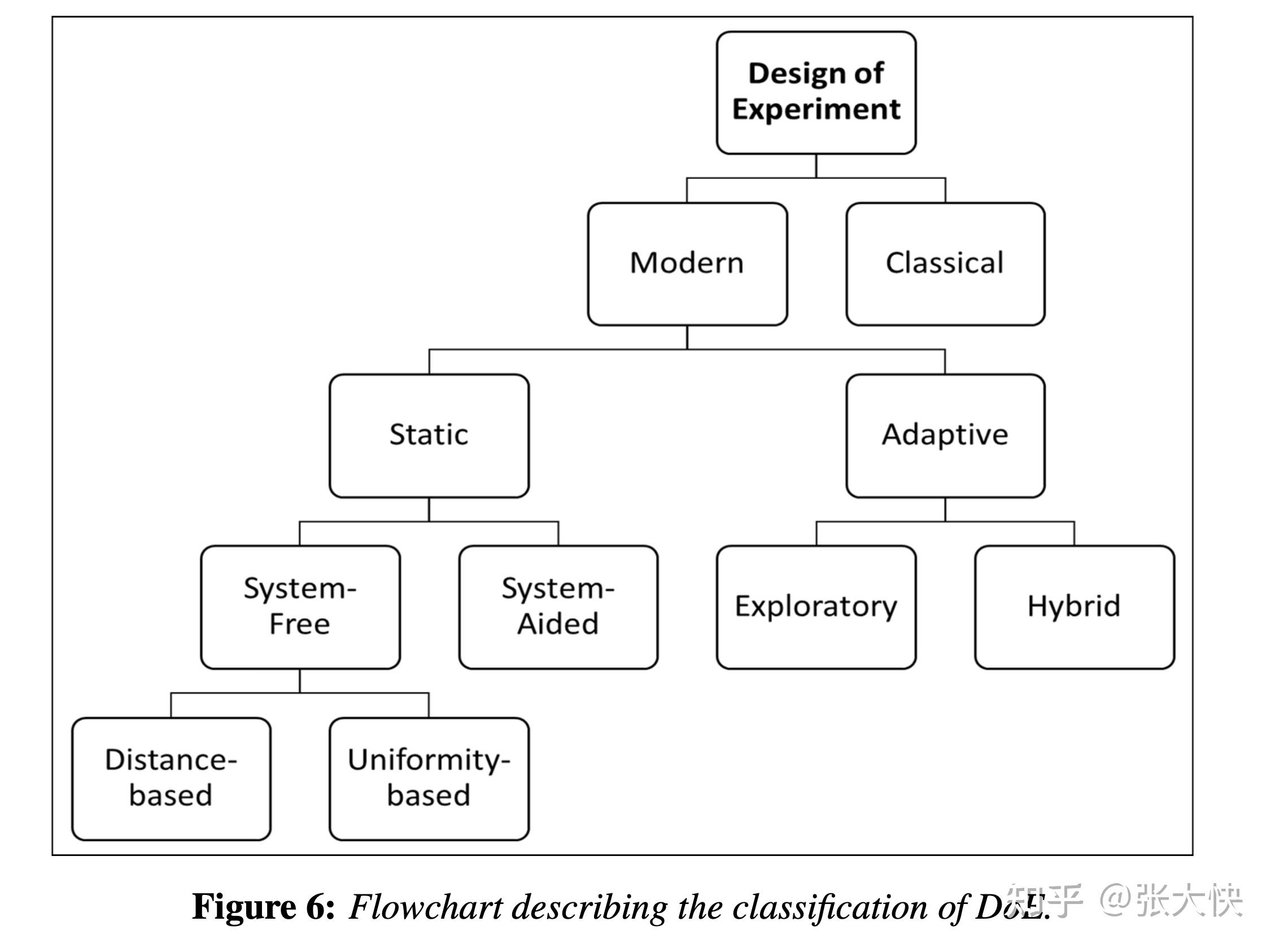
图3.2：实验设计的分类树

在超参数优化中一个重要的问题是在初始阶段如何有效的生成初始点集合。这个初始点集合一般来说有如下的要求：

在定义域分布均匀；
相邻的维度相关性小，特别是在高维情况；
计算速度快。

3.2 实验设计空间

定义实验设计空间，

$\begin{aligned} x&=\{x_i|i=1,2,...,d \} \in \mathbb{R}^d\\ x^{L}& \leq x \leq x^{U} \\ 即x_{i}^{L}& \leq x_{i} \leq x_{i}^{U} ,i=1,2,...,d \\ \end{aligned} \\$
通常为了避免数值不稳定，我们将其转化至空间 $[0,1]^d$ 。我们采样个点及其对应的函数值：

$\begin{aligned} X_{N}^{K} &= \{ x^{(k)} | k=1,2,...,K\}\\ Y^{K} &= \{ y^{(k)} | k=1,2,...,K\}\\ \end{aligned} \\$
3.3 点集偏差

在超参数(黑盒)优化初始阶段，需要从实验设计空间中采样若干个点作为初始点集，记为。如何评估我们采样点集 $S$ 的质量呢？我们在对求解的黑盒函数一无所知的时候，最占优的策略是从实验设计空间均匀的采样，这点和机器学习的最大熵原理类似。
评估采样点集的好坏，可以通过点集偏差来评估。通俗讲，偏差是评估采样点集生成均匀程度的度量，偏差越小，生成的点集质量越好。

图3.3：伪随机序列(左)和低偏差序列(右)对比

本节关于一维点集偏差，任意有界区域中的点集偏差内容主要参考了朱尧辰《点集偏差引论》[19]。
3.3.1 一维点集偏差

设 $\mathbb{S}=\{ a_1,..., a_n\}$ 是单位区间[0,1)的一个实数列，对于任意的 $\alpha,\beta \in [0,1]$ ，且 $\alpha < \beta$ ,用 $A([\alpha,\beta);n)=A([\alpha,\beta);n;\mathbb{S})$ 表示这个数列落在区间 $[\alpha,\beta)$ 中项的个数，称：

$D_{n} = D_{n}(\mathbb{S}) = \sup_{0\leq\alpha < \beta \leq 1} |\frac{A([\alpha,\beta);n;\mathbb{S})}{n} - \frac{(\beta -\alpha )}{1} | \tag{10}$
为数列的偏差[19]。 $D_{n}(\mathbb{S})$ 是数列在 $[0,1)$ 中分布的均匀程度的刻画。
令：

$D_{n}^{*} = D_{n}^{*}(\mathbb{S}) = \sup_{0 < \alpha \leq 1} |\frac{A([0,\alpha);n;\mathbb{S})}{n} - \frac{\alpha }{1} | \tag{11}$
称其为数列的星偏差。
3.3.2 任意有界区域中的点集偏差

表示任意的 $d(>1)$ 维有界区域，其体积 $|D|>0$ ，用表示中所有的维平行体（即平行于坐标轴的维长方体)(其体积 $|P|>0$ )的集合，设 $\mathbb{S}=\mathbb{S_{d}}=\{x_1,...,x_n \}$ 是中的一个有限点列，用表示落在平行体中的点的个数，则：

$D_{n} = D_{n}(\mathbb{P},D) = \sup_{0\leq\alpha < \beta \leq 1} |\frac{A(P;n;\mathbb{P})}{n} - \frac{|P|}{|D|} | \tag{12}$
为点列在中的偏差[19]。其中：

第1个式子表示落在平行体中的点的个数和的个数比；
第2个式子任意平行体和实验设计空间的体积比。

上式的含义是对于的任意平行体，个数比和体积比的差集上界越小，空间填充越均匀。
3.4 拟蒙特卡洛采样

随机序列的生成可以大致分为如下两类：

伪随机序列：其均匀性是随机均匀性，如目前广泛使用的线性同余生成器；
拟随机序列：其均匀性是等分布均匀性，如van Der Corput序列、Halton序列、Faure序列及Sobol序列。

用拟随机数代替随机数进行蒙特卡洛模拟，称为拟蒙特卡洛方法（采样）。
3.4.1 低偏差序列

在最坏的情况下，满足下面条件的拟随机数序列称为低偏差序列(quasi-random low discrepancy ，QRLD)[20]

$D_{n}^{*} \leq c_{d} ln^{d} n /n \\$
其中 $c_{d}$ 是与无关的常数。
从上图6可以看到，低偏差序列能够产生较均匀的实验设计点集列，其质量由上面的理论上界来保证。
拟随机数序列是低偏差序列。低偏差序列通过将一系列的整数表示成某个基radix(base)的位数形式：

$\begin{aligned} I &= I_{0} + I_{1} R + I_{2} R^2 + ... + I_{Q} R^Q \\ 其中I &\equiv I_{Q}I_{Q-1}...I_{1}I_{0}，\mathbb{Q} = \{1,2,...Q\}, \mathbb{Q} \subseteq N \end{aligned} \tag{13}$
定义基逆函数：

$\begin{aligned} \theta_{R}(I) &= .I_{0}I_{1}...I_{q}\\ \theta_{R}(I) & =I_{0} + I_{1} R^{-1} + I_{2} R^{-2} + ... + I_{q} R^{-q-1}\\ &= (I_{0},I_{1},...,I_{q} ) \cdot ( 1, R^{-1},R^{-2},...,R^{-q-1})^T \end{aligned} \tag{14}$

van Der Corput 序列采样

$S=\{ \theta_{R}(k) |k = 1,2,...,K \} \tag{15}$

Hammersley 序列采样

$\begin{aligned} z_{N}^{(k)}&=( \frac{k}{K} ,\theta_{2}(k), \theta_{3}(k),...,\theta_{R_{n-1}}(k) ) ,k = 1,2,...,K\\ x_{N}^{(k)}&= 1 - z_{N}^{(k)} ，为Hammersley 序列 \end{aligned} \tag{16}$
其中是第前个素数。

Halton序列采样

$S= \{ (\theta_{R_1}(k), \theta_{R_2}(k),...,\theta_{R_{n-1}}(k) ) | k=1,2,...,K\} \tag{17}$
其中为前个素数。

Sobol序列采样 Sobol序列生成的原理和Halton类似，但Sobal固定radix(base) = 2。相比Halton序列的差异点是在翻转前乘以一个矩阵 $C$ ，即方向数(Direction Numbers)：

$\begin{aligned} \theta_{R}(I) &= (I_{0},I_{1},...,I_{q} ) \cdot C \cdot ( 1, R^{-1},R^{-2},...,R^{-q-1})^T \end{aligned} \tag{18}$
同时它引入了方向数(Direction Numbers)来构造生成序列。

图3.4：随机序列 V.S. Sobol序列

van Der Corput序列、Hammersley序列、Halton序列和Sobol序列的星偏差上界可以参考[19][20]
3.4.2 低偏差序列适用场景

Halton序列在在 $N\geq 14$ 的情况下容易产生高度从聚和相关的样本，使得求解的黑灰函数容易陷入局部最优解。在实际使用中建议Halton序列在 $N< 8$ 维下使用。我们在QQ浏览器超参数比赛中，因为测试的维度 $N \leq 3$ ，表现好于拉丁超立方，在提交算法也使用Halton序列，实际线上评估数据可能是超高维的，算法可能会陷入局部最优解。

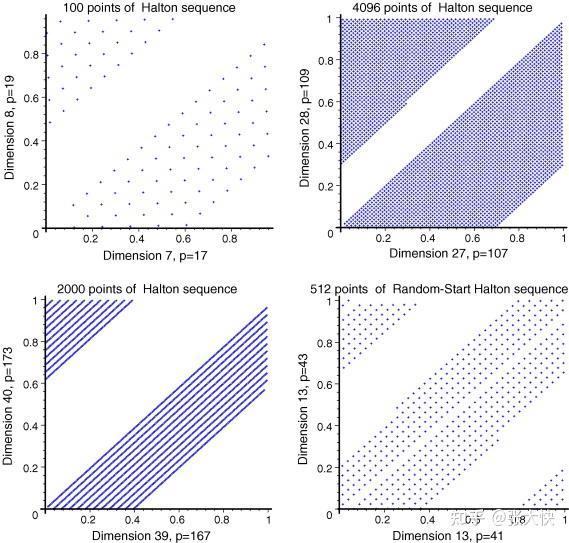
图3.5：Halton序列从聚现象

上面我们讨论的几种常见的拟随机序列其适用：

3.5 拉丁超立方采样

本节主要参考了[21]。假设我们的实验设计需要生成个点，其对应的矩阵形式为:

$X = [x_1,x_2,...,x_p]^T , x_i \in \mathbb{R}^N \\$
拉丁超立方方法是如何采样出这样应该一个矩阵呢？它的具体做法如下：将个维度的每一维等分成个桶(bin)，每个桶里面有且只有一个点。通过这种方式，我们就能生成相应的个点。

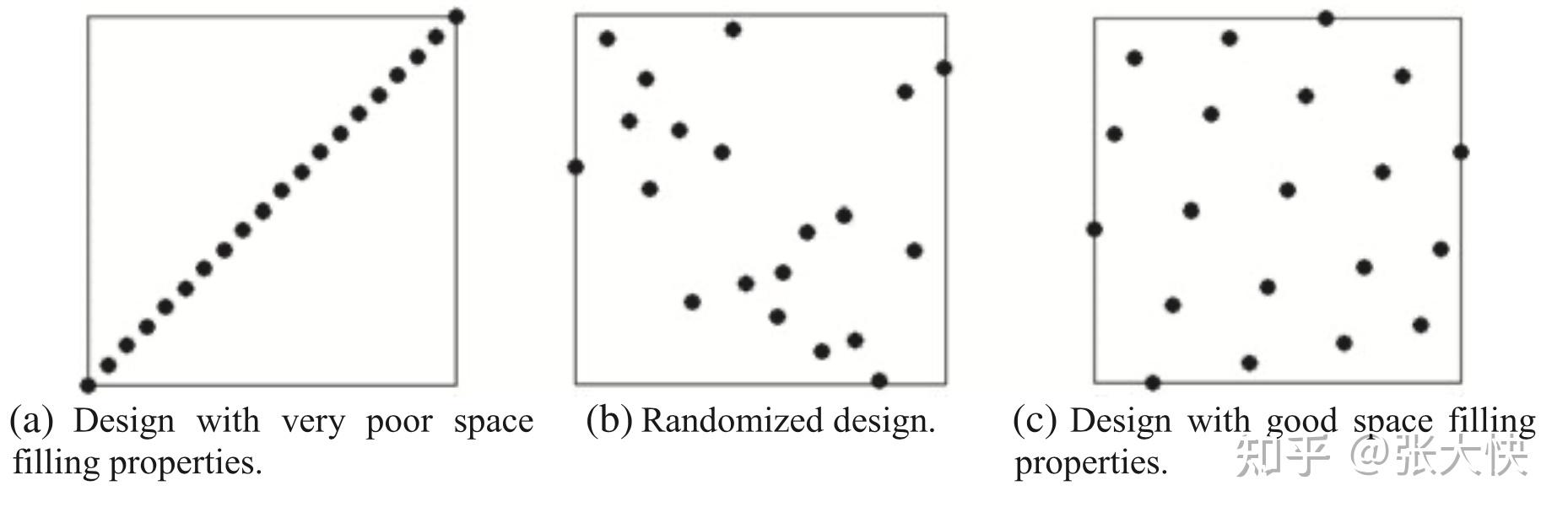
图3.6：拉丁超立方采样序列

上图展示了拉丁超立方在 $N=2$ 维空间内生成 $p=20$ 个点的情形：

图9-a是最坏的情形；
图9-b是随机情形，呈现随机性；
图9-c是拉丁超立方采样，呈现均匀性。

3.5.1 关于拉丁超立方的几个问题

问题1：为什么拉丁超立方会为大家喜爱
一个好的的采样算法，需要满足如下的条件：

生成的采样点，能够适应不同的统计假设；
生成的采样点，能够覆盖由小到大的设计空间。

拉丁超立方恰好能满足上面两点，使得它能成为一种有效的实验设计方法。
另外一个原因是拉丁超立方具有较好的可扩展性，非退化的(Non-collapsing)：将维空间去掉若干维，剩余维度构成的样本，仍然是一个拉丁超立方样本。

图3.7：拉丁超立方序列非退化性

如上图所示，两种方法生成15个样本点：

图10-a中的拉丁超立方方法，，去掉任意其中一维，剩余空间的样本点个数仍然是15；
图10-b中的中心合成设计方法(Central composite design)，，去掉任意其中一维，剩余空间的样本点个数减少至9。

问题2：拉丁超立方的用处有多广泛？
正如我们前面提到，拉丁超立方方法是和模型无关的，也不会假设拉丁超立方生成点和模型输出有较大的相关性。基于拉丁超立方的优化问题，实际上是个组合优化问题：个样本点、维空间，其对应的空间复杂度为 $O(p!^d)$ 。单独使用拉丁超立方方法求解黑盒问题，实际上并不高效，需要结合其他的优化方法才能进行有效的搜索，这是本系列文章后续讨论的内容。
问题3：拉丁超立方有什么缺点呢？
在工业设计中，我们可能需要将原实验设计空间(维)，迁移到目标实验设计空间总去():

当 $M \leq N$ 时，由拉丁超立方的非退化性，原实验设计空间建模可以复用在目标实验设计空间去；但不能保证在原空间求得的最优解可以复用在目标实验设计空间去；
当 $M \geq N$ 时，此时原实验设计空间建模不能复用在目标实验设计空间，需要重新建模。

问题4：当我们进行实验设计时，拉丁超立方总是可以使用的吗？
答案是依据我们求解的问题而定。正如我们在讨论HEBO的章节中所说的，没有”一招鲜吃遍天“的方法。我们可以尝试多种方法，或者将他们组合来用，更好的服务于我们需要求解的问题。
实验设计的开源实现，可以参考pyDOE2：https://github.com/clicumu/pyDOE2
四、TuRBO：基于信赖域的贝叶斯优化

摘要：TuRBO是一种全局优化方法，通过构建一系列的局部GPs代理模型，从全局角度能够避免过度探索(Exploitation)；同时在局部能够充分利用信赖方法的二阶收敛性，进行高效的求解(Exploitation)。TuRBO方法近年来在机器学习超参数优化中表现效果优异，本文介绍了其原理和代码详解。
本节内容参考了[7]: Eriksson, David, et al. &#34;Scalable global optimization via local bayesian optimization.&#34; Advances in Neural Information Processing Systems 32 (2019): 5496-5507.
4.1 简介

在贝叶斯优化中，我们通常尝试构建一个全局模型；全局模型过度强调了探索(Exploration)，在高维场景中，不能很好的进行利用(Exploitation)。高维黑盒问题优化，通常面临如下的问题：

随着求解问题维数增大，难度呈指数增长；局部最优解将变得非常的稠密，寻找全局最优解将变得困难；
黑盒函数通常是各种各样的，很难找到一个全局的代理模型来近似；
搜索空间相比于采样点个数(Budget)，随着维数的增大将变得巨大。

TuRBO方法结合了信赖域和贝叶斯优化，近年来在机器学习超参数优化中表现效果优异。其主要的思想：

基于当前的评估点集，构建GPs代理模型；
选取当前最小点，以GPs代理模型的作为权重半径，构建信赖域；
在信赖域内，随机抽样若干个点；用GPs模型预测出最大后验候选点集；
根据当前最大候选点集的函数值，增大或者缩小信赖域半径；
结束条件：信赖域半径小于给定值或者大于给定次数。

TuRBO是一种全局优化方法，通过构建一系列的局部GPs代理模型，从全局角度能够避免过度探索(Exploitation)；同时在局部能够充分利用信赖方法的二阶收敛性，进行高效的求解(Exploitation)。
4.2 信赖域方法

信赖域方法有着较好的收敛性、稳定性和适用性，在无约束优化中有较广泛的应用。本节内容主要参考了[12]
4.2.1 无约束优化问题

考虑如下的无约束优化问题：

$\begin{aligned} \min_{x} \enspace f(x) ,x \in R^N \\ \end{aligned} \tag{19}$
其中，的取值为n维实数空间 $R^n$ ，为连续一阶可导函数。
无约束优化问题求解方法，大致分成两类：

不限定搜索区域：如线性搜索，根据搜索的方向，可分为梯度法、牛顿法和拟牛顿法；
限定搜索区域：如信赖域方法，信赖域方法是二阶方法。

上述两类方法都依赖于函数在某一点附近的泰勒展开
4.2.2 问题定义

给定无约束优化问题 $(19)$ ，其在处的泰勒展开式：

$\begin{aligned} f(x_k + d ) = f_k + g_k^Td +\frac{1}{2} d^T \nabla^2 f(x_k +td)d ,x \in R^N \end{aligned} \tag{20}$
其中 $f_k = f(x_k), g_k = \nabla f(x_k),t\in(0,1)$ , $t$ 为和有关的正数。我们使用和 $Hessian$ 矩阵的近似 $B_k$ 来作为二次项，则上式重写为：

$\begin{aligned} m_k(d ) = f_k + g_k^Td +\frac{1}{2} d^TB_k d \\ \end{aligned} \tag{21}$
模型 $m_k(d )$ 和待优化函数 $f(x_k+d)$ 之间的差异为： $O(||d||^2)$
模型 $m_k(d)$ 在处能近似 ,仅当较小时有意义。信赖域方法将限定在以为中心的球内：

$\begin{aligned} \Omega_K = \{x_k + d | \enspace ||d|| \leq \Delta_k \} \end{aligned} \tag{22}$
其中 $\Omega_K$ 为信赖域、为信赖域半径。有了上面的定义后，信赖域方法每步需要求解如下的子问题：

$\begin{aligned} \min_{d\in R }\enspace &m_k(d ) = f_k + g_k^Td +\frac{1}{2} d^TB_k d \\ \text{s.t. } \enspace & ||d|| \leq \Delta_k\\ \end{aligned} \tag{23}$
子问题的解 $d_k^*$ （下降方向）就是模型在信赖域半径范围内的最小解，。
信赖域方法迭代中，一个重要的问题是，每一步如何选取信赖域半径大小。一般的考虑是前一步迭代中，模型函数和目标函数的近似情况。
给定当前求解的，我们定义比值：

$\begin{aligned} \rho_k = \frac{f(x_k) - f(x_k+d_k)}{m_k(0) - m_k (d_k)} \end{aligned} \tag{24}$
其中，分子为目标函数下降的量；分母为模型函数预期下降的量。
我们根据 $\rho_k$ 取值，分如下4种情况讨论：

$\rho_k < 0$ ，则目标函数 $f(x_k+d_k)$ 大于当前的目标函数值，则下降方向无效，需要缩小当前信赖域半径；
$\rho_k \approx 0$ ，缩小当前信赖域半径；
$\rho_k \approx 1$ ，则说明模型函数和目标函数一致，下一步迭代中可以扩大信赖域的半径；
$\rho_k>0$ 且显著小于1时，不改变信赖域半径大小。

信赖域算法如下[12] :

图4.1：信赖域算法迭代步骤

4.3 TuRBO原理

参考了TuRBO的论文和代码，我们这里直接给出了TuRBO的算法流程，接下来将详细介绍每一步的细节。源码：https://github.com/uber-research/TuRBO/blob/master/turbo/turbo_1.py

图4.2：TuRBO：基于信赖域的贝叶斯优化方法

def optimize(self):
      &#34;&#34;&#34;Run the full optimization process.&#34;&#34;&#34;
      while self.n_evals < self.max_evals:
         if len(self._fX) > 0 and self.verbose:
            n_evals, fbest = self.n_evals, self._fX.min()
            print(f&#34;{n_evals}) Restarting with fbest = {fbest:.4}&#34;)
            sys.stdout.flush()

         # Initialize parameters
         self._restart()

         # Generate and evalute initial design points
         X_init = latin_hypercube(self.n_init, self.dim)
         X_init = from_unit_cube(X_init, self.lb, self.ub)
         fX_init = np.array([[self.f(x)] for x in X_init])

         # Update budget and set as initial data for this TR
         self.n_evals += self.n_init
         self._X = deepcopy(X_init)
         self._fX = deepcopy(fX_init)

         # Append data to the global history
         self.X = np.vstack((self.X, deepcopy(X_init)))
         self.fX = np.vstack((self.fX, deepcopy(fX_init)))

         if self.verbose:
            fbest = self._fX.min()
            print(f&#34;Starting from fbest = {fbest:.4}&#34;)
            sys.stdout.flush()

         # Thompson sample to get next suggestions
         while self.n_evals < self.max_evals and self.length >= self.length_min:
            # Warp inputs
            X = to_unit_cube(deepcopy(self._X), self.lb, self.ub)

            # Standardize values
            fX = deepcopy(self._fX).ravel()

            # Create th next batch
            X_cand, y_cand, _ = self._create_candidates(
                  X, fX, length=self.length, n_training_steps=self.n_training_steps, hypers={}
            )
            X_next = self._select_candidates(X_cand, y_cand)

            # Undo the warping
            X_next = from_unit_cube(X_next, self.lb, self.ub)

            # Evaluate batch
            fX_next = np.array([[self.f(x)] for x in X_next])

            # Update trust region
            self._adjust_length(fX_next)

            # Update budget and append data
            self.n_evals += self.batch_size
            self._X = np.vstack((self._X, X_next))
            self._fX = np.vstack((self._fX, fX_next))

            if self.verbose and fX_next.min() < self.fX.min():
                  n_evals, fbest = self.n_evals, fX_next.min()
                  print(f&#34;{n_evals}) New best: {fbest:.4}&#34;)
                  sys.stdout.flush()

            # Append data to the global history
            self.X = np.vstack((self.X, deepcopy(X_next)))
            self.fX = np.vstack((self.fX, deepcopy(fX_next)))

下面我们逐步按构建候选点、筛选最优候选点、调整信赖域半径三部分来介绍。
4.3.1 构建候选点

参考源码中的函数：
self._create_candidates(
                  X, fX, length=self.length, n_training_steps=self.n_training_steps, hypers={}
            )
算法的主要步骤：

基于当前评估点集 $X,fX$ ，构建高斯过程回归模型(GPs)，获得模型的值作为权重 $weight$ ；
取当前最优函数值 $min(fX)$ 对应的点作为中心点 $x_{center}$ ，构建新的超立方球，超立方球的上界、下界由下面的公式定义（length为信赖域半径）：

$lb = np.clip(x_{center} - weights * length / 2.0, 0.0, 1.0) \\ ub = np.clip(x_{center} + weights * length / 2.0, 0.0, 1.0) \\$

调用torch的sobol算法生成个拟随机序列候选点；
调用GPs模型对个候选点进行最大似然估计，输出个候选点及其对应的函数值。

4.3.2 筛选最优候选点

参考源码中的函数：
X_next = self._select_candidates(X_cand, y_cand)
在调用create_candidates生成个候选点后，我们接着调用select_candidates筛选出batch_size（这里为一次suggest的候选个数，如5）个最优候选点
4.3.3 调整信赖域半径

参考源码中的函数：
self._adjust_length(fX_next)
根据前面生成的最值 $min(y_{cand})$ ,调整信赖域的半径：

如果当前最优值 $min(y_{cand})< y_{best}$ ，则搜索成功次数增加1： $succcount += 1$ ，否则失败次数 $failcount += 1$ ；
信赖域半径扩大条件（乘以2）：如果当前成功次数等于预先设置的阈值( $succtol=3$ ): ；
信赖域半径缩小条件（除以2）：如果当前失败次数等于预先设置的阈值( $failtol=3$ ，和维度及batch_size有关):

4.4 总结

在2020 NeurIPS 举办了黑盒优化的比赛 [2] 中，在128个评估点集下，TuRBO方法在作为单个求解算法，是非常的优秀的:

图4.3：2020 BBO 比赛单个求解器性能

如果将评估点限定为50个，在QQ浏览器超参数优化比赛中，我们将看到TuRBO方法因为收敛较晚，效果也下降了。
五、MCTS+TuRBO：基于蒙特卡洛树搜索的贝叶斯优化

摘要：本文介绍了一种基于蒙特卡洛树搜索MCST+TuRBO的黑盒函数优化方法。主要的思想是在全局函数空间，通过二叉树递归的将函数空间划分为高函数值和低函数值两部分；能够有效的对高潜力的函数空间进行搜索，特别是在高维情况；在上述方法划分出的局部空间内，使用基于信赖域的二阶求解方法进行高效的求解。
5.1 背景

在黑盒函数优化中：

$\begin{aligned} \arg min_{x\in X} \enspace f(x) \end{aligned} \tag{25}$
我们通常面临着函数搜索空间巨大（N的维数非常高）黑盒函数为高度非线性（highly nonlinear)，在有限的时间和资源条件下，比较难进行有效的搜索。
论文[6]提出了一种基于空间划分+局部建模优化的方法。主要的思想：

基于蒙特卡洛树搜索空间划分。通过二叉树，递归的将函数空间划分为高函数值和低函数值两部分；在每次函数空间划分时，通过聚类算法聚成两类（高潜力点、低潜力点），使用两类类别信息构建出非线性的决策面（SVM）,能够有效的对高潜力的函数空间进行搜索，特别是在高维情况；
在局部空间使用TuRBO进行求解。在上述方法划分出的局部空间内，使用基于信赖域的二阶求解方法进行高效的求解。

为了方便叙述，我们假定我们已经通过实验设计的方法获得了评估点集：

$D_{0} = \{ x_i, f(x_i) \}, i=1,...,M \\$
进一步我们可以将MCST+TuRBO方法分成3步：

第1步：树构建（训练阶段），核心是对搜索空间进行有效划分；
第2步：树搜索（预测阶段），从评估点集中筛选出高潜力点；
第3步：TuRBO方法（精确求解），从第2步的高潜力点的信赖域半径内搜索出下一高潜力点。

论文[7]是在2020 NeurIPS BBO 比赛中的一种实现。我们将结合论文[6]及[7]的源码，按照上面3步进行详细的介绍。
5.2 蒙特卡洛树构建（MCT)

从何角度来理解蒙特卡洛树搜索呢？经典的蒙特卡罗方法的三个主要步骤：

构造或描述概率过程；
实现从已知概率分布抽样；
建立各种估计量。

经典的蒙特卡洛树构建，包含了4个步骤：

选择(Selection)：从当前节点(R)选择一个子节点(E,随机或者根据UCB) ；
拓展(Expansion)：对节点E进行拓展。选择和拓展生成下图的Default Policy ；
模拟(Simulation)：从扩展的E节点出发，进行模拟（生成一系列的子节点），模拟结束后计算节点E的reward
反向传播(Backpropagation)：将E的reward回传给父节点

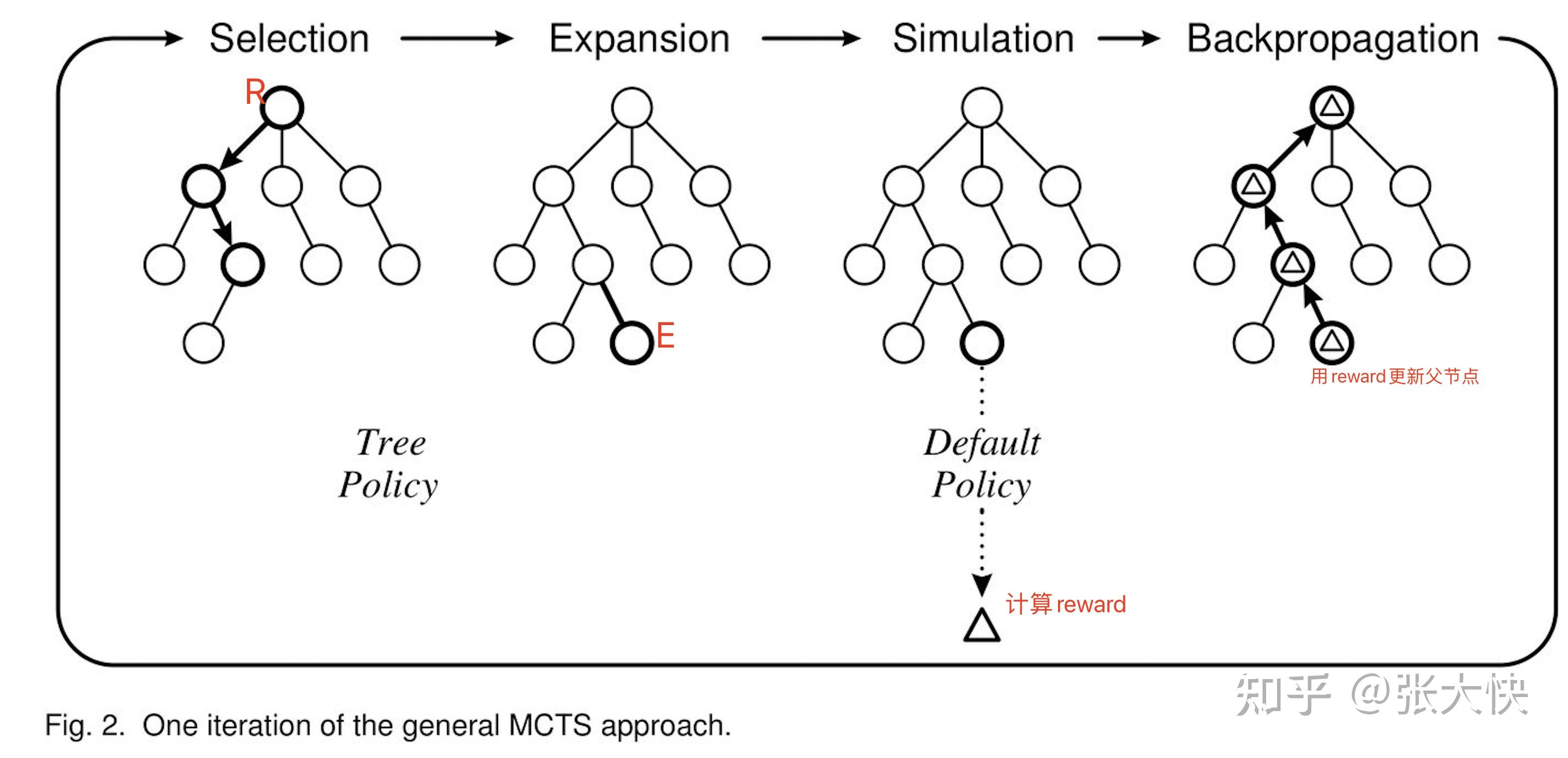
图5.1：经典蒙特卡洛树构建

论文[6]提出的LA-MCTS构建，包含了3个步骤：

学习和分裂(Learning & Splitting ): 基于当前获得的评估点集，学习和构建LA-MCTS搜索树（包含Kmeans聚类和SVM分类器构建决策面)，搜索树的每个节点是一个SVM分类器;
选择函数空间(Select)：简单的策略是直接选择最左子树，但容易陷入局部最优解，作者引入UCB来进行选择；
采样(Sampling )：在上面选择的函数空间内（叶子节点)，使用BO的方法，生成下一高潜力点。

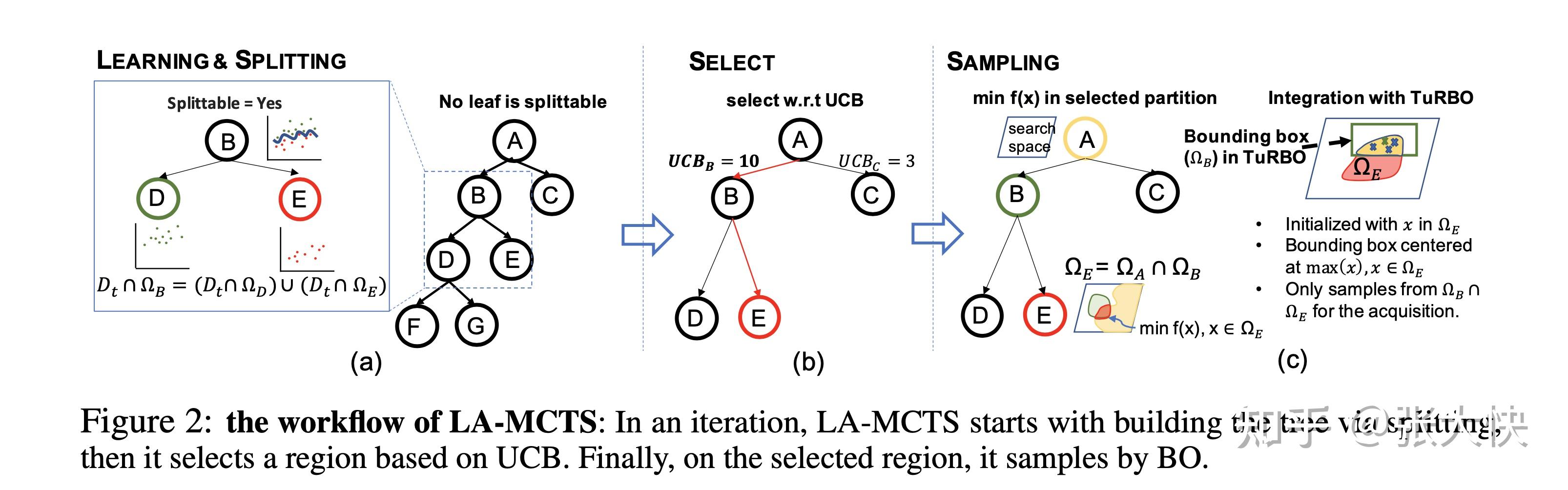
图5.2：经典蒙特卡洛树构建

5.2.1 树构建

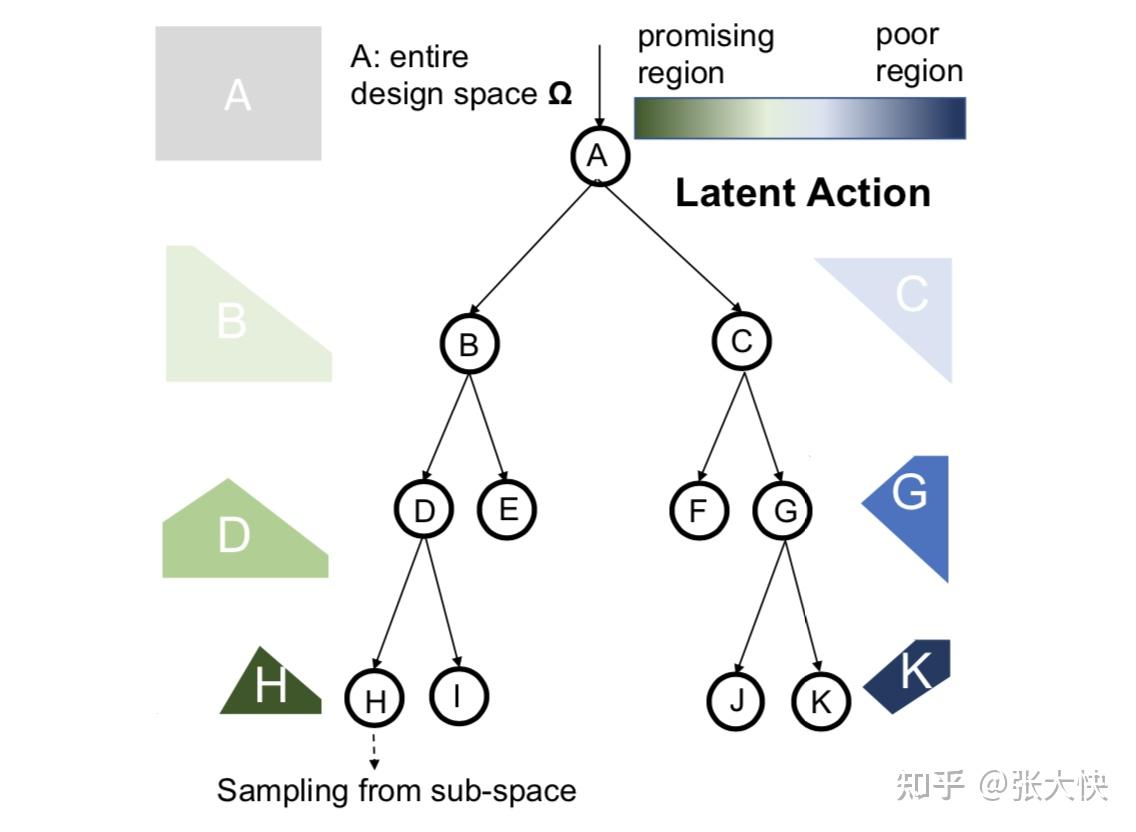
图5.3：学习空间划分

如上图所示，假设我们已经获得了评估点集，我们根据N个样本点构建一颗二叉树来对搜索空间进行划分。约定左子树是高潜力区域，右子树是低潜力区域：

从根节点到最左的叶子节点H是最高潜力区域
从根节点到最右的叶子节点K是最低潜力区域

通过树节点的不断分裂，将整个空间A划分出了若干的区域。当评估点集数量 $|D_{0}|$ 较少时，划分出蒙特卡洛搜索树将不置信。对样本点有如下的两个基本要求：

样本点数量要有一定量级，如 $|D_{0}| \geq 10$ ；
样本点在搜索空间中分布均匀，即需要有个较好的实验设计，具体可用参考笔者前面文章

5.2.2 树节点分裂

上面树的构建中，有一个比较重要的问题是每一次节点是如何分裂生成左子树和右子树的呢？主要分为3步：

第1步，聚类：根据落在当前节点的样本（设为 $N(N\leq M)$ 个），使用Kmeans聚类，将个样本划分为个高潜力样本( $label = 1$ ) 、个低潜力样本( $label = 0$ ): $N=N_{high} + N_{low}$ ；
第2步，分类：根据第1步的 $label$ 信息，构建 $SVM$ 分类器，学习出当前节点的决策面(Boundary)；
第3步，递归：递归的将当前个结点分裂成左子树，将当前结点分裂成右子树。

详细见下图

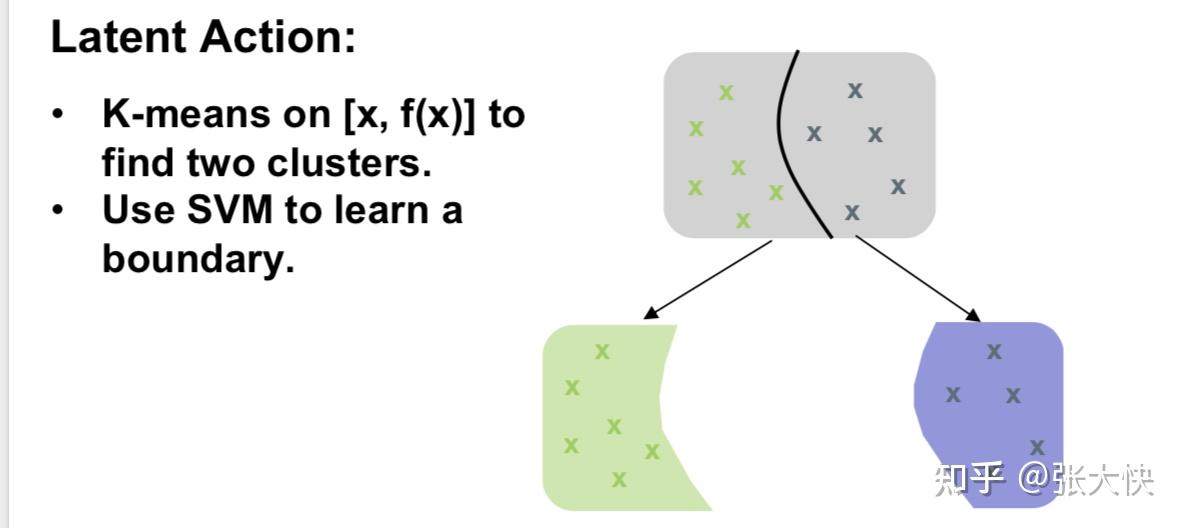
图5.4：MCTS 树节点分裂

5.3 蒙特卡洛树搜索（MCTS)
在上面构建好一颗蒙特卡洛树后，我们如何进行搜索，探测下一个高潜力节点呢？假设当前构建的蒙特卡洛树，从根节点到最左叶子节点的深度为。（注：因我们关注的是高潜力节点，右子树节点为低潜力节点，实际可以不分裂，搁置不管，我们后面介绍的代码实现[7]也是这个策略）给定当前的个评估点集，我们从根节点出发到最左叶子节点，落在每个节点的评估点集数量为，得到序列 $\{m_1,m_2,...m_k,...,m_K\}$ :

$M \geq m_1 \geq m_2 ... \geq m_K$
高潜力评估点集数量为 $m_K$ ,设为

5.4 TuRBO求解

我们根据上面筛选的高潜力评估点集，将输入到TuRBO中进行求解，筛选出下一高潜力候选点。 TURbo求解，可以参考笔者文章：
5.5 MCTS+TuRBO代码解析

源代码[7]：https://github.com/jbr-ai-labs/bbo-challenge-jetbrains-research/blob/master/submissions/space-decay/optimizer.py
5.5.1 MCTS树构建

主要的步骤：

对评估点集，使用Kmeans聚类，SVM进行决策面划分
预测当前候选点X落在高潜力区域的数量
筛选高潜力候选
筛选低潜力候选
高潜力候选点，递归构建搜索树
返回构建好的MCTS树

  def _build_tree(self, X, y, depth=0):
print(&#39;len(X) in _build_tree is&#39;, len(X))
if depth == self.config[&#39;max_tree_depth&#39;]:
   return []
split = self._find_split(X, y) # 1. 对评估点集$D_{0}$ 使用Kmeans聚类，SVM进行决策面划分
if split is None:
   return []
in_region_points = split.predict(X)# 2. 预测当前候选点X落在高潜力区域的数量
left_subtree_size = np.count_nonzero(in_region_points == 1)# 3. 筛选高潜力候选点
right_subtree_size = np.count_nonzero(in_region_points == 0)# 4. 筛选低潜力候选点
print(f&#39;{len(X)} points would be split {left_subtree_size}/{right_subtree_size}.&#39;)
if left_subtree_size < self.n_init:
   return []
idx = (in_region_points == 1)
splits = self._build_tree(X[idx], y[idx], depth + 1)# 5. 高潜力候选点，递归构建搜索树
return [split] + splits # 6. 返回构建好的MCTS树
5.5.2 获得下一高潜力候选点

主要的步骤：

构建MCTS搜索树、构建TURbo
获得落在高潜力区域的候选点
从高潜力候选点出发，生成下一高潜力候选点
使用GPs + sobol构建候选点集
使用MCTS，获取候选点集的高潜力候选点
高潜力候选点择优

def _suggest(self, n_suggestions):
X = to_unit_cube(deepcopy(self.X), self.lb, self.ub)
y = deepcopy(self.y)
if not self.node:
   # 1. 构建MCTS搜索树、构建TURbo
else:
   # 2. 获得落在高潜力区域的候选点
   idx = (self._get_in_node_region(X, self.node) == 1)
   X = X[idx]
   y = y[idx]

length_reties = self.config[&#39;turbo_length_retries&#39;]
for retry in range(length_reties):
   # 3. 从高潜力候选点出发，生成下一高潜力候选点
   XX = X
   yy = copula_standardize(y.ravel()) # 函数值标准化
   # 4. 使用GPs + sobol构建候选点集
   X_cand, y_cand, _ = self.turbo._create_candidates(
      XX, yy, length=length, n_training_steps=self.config[&#39;turbo_training_steps&#39;], hypers={})
   # 5. 使用MCTS，获取候选点集的高潜力候选点
   in_region_predictions = self._get_in_node_region(X_cand, self.node)
   in_region_idx = in_region_predictions == 1
   if DEBUG:
      print(f&#39;In region: {np.sum(in_region_idx)} out of {len(X_cand)}&#39;)
   if np.sum(in_region_idx) >= n_suggestions:
      X_cand, y_cand = X_cand[in_region_idx], y_cand[in_region_idx]
      self.turbo.f_var = self.turbo.f_var[in_region_idx]
      if DEBUG:
      print(&#39;Found a suitable set of candidates.&#39;)
      break
   else:
      length /= 2
      if DEBUG:
      print(f&#39;Retrying {retry + 1}/{length_reties} time&#39;)
# 6. 高潜力候选点择优
X_cand = self.turbo._select_candidates(X_cand, y_cand)[:n_suggestions, :]

return X_cand
5.6 总结

本文介绍了一种基于蒙特卡洛搜索树MCST+TuRBO的黑盒函数优化方法[6][7]。主要的思想：

在全局函数空间，通过二叉树递归的将函数空间划分为高函数值和低函数值两部分；在每次函数空间划分时，通过聚类算法聚成两类（高潜力点、低潜力点），使用两类类别信息构建出非线性的决策面（SVM）,能够有效的对高潜力的函数空间进行搜索，特别是在高维情况；
在局部空间使用TuRBO进行求解。在上述方法划分出的局部空间内，使用基于信赖域的二阶求解方法进行高效的求解。

笔者在QQ浏览器2021AI算法大赛使用了该方法，MCST+TuRBO在全局空间的探索上，表现出色；当问题有较多的局部最优解时，容易陷入局部最优解，跳不出来。后面我们介绍的《HEBO：异质方差进化贝叶斯优化》、《pySOT和POAP: 代理模型优化工具箱及其异步并行框架》将在一定程度上弥补MCST+TuRBO的不足。
六、HEBO：异质方差进化贝叶斯优化

摘要：HEBO通过分析经典贝叶斯优化中数据输入、数据输出、代理模型和采集函数存在的问题和局限性，并对每一个问题做了相应的优化：对数据输入、数据输出进行变换校准；将数据变换校准和GPs核函数一起联合优化；引入多目标采集函数，对候选点进行更鲁棒的探索。
6.1 背景

近年来，贝叶斯优化在求解黑盒函数问题中应用越来越广泛。使用贝叶斯优化来求解黑盒函数问题通常会做一些较为严格的假设。

建模假设，使用代理模型来近似黑盒函数问题。常见的代理模型是高斯过程回归模型（Gaussian processes，GPs)。GPs模型本身是同方差的（Heteroscedastic），但其实际建模的问题是带异质方差噪音，同时同方差的GPs模型不能处理非平稳的评估点集，这种现象在机器学习超参数优化中尤为常见。
采集函数和优化器假设。在采集函数阶段，通常是最大化采集函数并输出下一个候选点。这一过程将引入额外的限制和假设。如假设黑盒函数中只包含连续变量，采取一阶或二阶（如LBFGS，ADAM）来求解，而忽略了超参数优化中包含的离散变量（如深度网络中的隐层大小）。另外在整一个贝叶斯优化框架中采集函数只选择一种，忽略了多个采集函数组合的情况。

6.2 贝叶斯优化建模思路

超参数优化可以看做是黑盒优化的一个例子：

$\arg min_{x\in X} \enspace f(x) \tag{26} \\$
其中，为超参数的一组设置取值，为混合设计空间(Design space)。为超参数优化中，我们需要优化的目标（如最小化loss)。
贝叶斯优化算法通过一系列的序列决策来近似全局最优值。在第 $i$ 轮的迭代中：

算法输出一个大小为的参数集合 $x_{1:q}^{new} \in X^q$ ，获取对应的函数值 $y_{1:q}^{new} = f(x_{1:q}^{new})$ ;
算法的目标是以最快的方式找到全局最优解 $x^* = \arg max_{x\in X} f(x)$ 。

为了达到这个目标，使用贝叶斯算法求解黑盒问题，通常分为两步：

第1步：学习一个贝叶斯模型（代理模型）；
第2步：通过采集函数来决定输出下一个采集点。

6.2.1 贝叶斯建模假设

当黑盒函数的自变量是连续值时，高斯过程回归模型(GPs)是一个非常高效的代理模型。对于黑盒函数，我们通常假设其符合某一个GPs先验分布。高斯过程回归模型(GPs)有如下的两方面来决定：

均值函数；
协方差函数(矩阵)，或者核函数 ,其中为核函数超参数。

有了上面的假设，我们通常假设观测到的函数值通过如下的形式产生：

$y_{l} = f(x_l) + \epsilon_{l}， where \enspace \epsilon_{l} \sim N(0,\sigma_{noise}^2 ) \tag{27}$
进而，可以得到高斯似然函数形式：

$y_{l}|x_{l} \sim N(f_l ,\sigma_{noise}^2 ) \tag{28}$
其中, 服从如下的分布：

$f(x) \sim GP(m(x),k_{\theta}(x,x^{'})) \tag{29}$
我们通常假设GPs的kernel 是平稳的，只依赖于两个点和之间的模，进一步假设在带噪音分布条件数据点是平稳的且同质的。如果我们观测的数据点不满足这个条件，我们将不能很好的近似黑盒函数。基于这点考虑，作者提出了两个问题：

问题1：超参数优化任务是平稳的吗？
问题2：超参数优化任务是同质的吗？

6.2.2 采集函数假设

给定先验和观察数据，我们可以得到相应的后验分布：

$后验分布= 先验分布 + 观察数据 \tag{30}$
采集函数是根据后验分布来构造的。在选取GPs作为代理模型条件下，其后验分布仍然是高斯分布：

$p(f(x_{1:q})| D) = N(\mu_{\theta}(x_{1:q}), \sum_{\theta}(x_{1:q})) \tag{31}$
接下来我们列出贝叶斯优化中常见的3种采集函数：

提升的概率 $(Probability\enspace improvement ,PI)$ :

$\alpha_{PI}^{\theta} (x_{1:q} | D ) = E_{post.}[\max_{j\in 1:q}\{H\{f(x_j) - f(x^+) \}\}] \tag{32}$
其中为左连续的阶跃函数或开关函数。采集函数的原理是在当前的邻域附近，找到比大的候选点，取这些概率最大的点，而不管比大多多少；

提升的期望 $(Expected\enspace Improvement ,EI)$ :

$\alpha_{EI}^{\theta} (x_{1:q}|D) = E_{post.}[\max_{j\in 1:q}\{ReLU(f(x_j) - f(x^+))\}]\tag{33}$
相比 $PI，EI$ 给出了下一候选点比当前最优值大多少的问题（提升期望)；

上置信边界 $(Upper\enspace confidence\enspace bound ，UCB)$ :

$\alpha_{UBC}^{\theta} (x_{j}) = E_{post.}[\max_{j\in 1:q}\{ \mu_{\theta} (x_j) - \sqrt{\beta \pi /2 } | \gamma_{\theta} (x_j) | \}] \tag{34}$
其中是后续点的后验均值，。
在贝叶斯优化算法建模中，我们通常选取上述函数中的一个作为代理模型的采集函数。这个采集函数相对于我们的代理模型和我们要优化的问题是否是最优的呢？
进一步我们有如下的问题：

问题3：在超参数优化中，不同采集函数输出的结果是否是冲突的呢？

6.3 模型假设分析及优化方案

6.3.1 问题1：超参数优化任务是平稳的吗？

回答：即使是简单的机器学习任务也显示出极大的非平稳性（ non-stationarity）

图6.1：输出校准

针对非平稳性，这里选取两种方式Box-Cox和Yeo-Jonhson来对输出进行校准(Transformation)：

如上图所示，对机器学习中的108个任务进行假设检验，对输入进行转换校准(transformations)后能较大的提升GPs建模的效果。
6.3.2 问题2：超参数优化任务是同质的吗？

回答：即使是简单的机器学习任务也显示出极大的异方差性（heteroscedasticity） 针对异质方差，这里选取两种方式Box-Cox和Yeo-Jonhson来对输出进行校准(Transformation)：

如上图所示，对机器学习中的108个任务进行假设检验，对输出进行转换校准(transformations)后能较大的提升GP建模的效果。
将问题1和问题2结合起来考虑，将会使我们得到更加健壮的GP模型：

其中，是GP模型的超参数， $\gamma$ 为对非平稳性进行转换， $\zeta^*$ 为Box-cox似然函数的解。其中 $K_{\theta}^{\gamma} \in R^{n\times n}$ 的矩阵，其元素为：

$K_{\theta}^\gamma(x,x^{'}) = k_{\theta} ( kumaraswamy_{\gamma}(x) , kumaraswamy_{\gamma}(x^{'}) ) \\$
6.3.3 问题3：在超参数优化中，不同采集函数输出的结果是否是冲突的呢？

回答：没有“一招鲜吃遍天”的方法。不同采集函数通常是冲突，经常会输出相反的候选点

图6.2：不同采集函数通常是冲突

如上图所示，不同采集函数在不同参数设置下，其对应的采集函数值相互冲突。对此，作者从如下两方面进行优化

带鲁棒性的采集函数；
多目标采集函数。

6.3.3.1 带鲁棒性的采集函数

在最大化采集函数阶段，我们通常假设选取的代理模型是能够充分刻画我们的问题空间的。在贝叶斯优化过程的初始阶段，数据非常稀缺，这个假设通常是很难验证的，导致我们对代理模型错误设定(model misspecification)，进而损害贝叶斯优化的性能。解决这种问题的一种方法是，在代理模型(GP)最坏的情形下，尝试找到最优的候选点，通过如下的优化方式实现:

$\max_{x} \min_{\theta} \alpha^{\theta}(x|D) \tag{35}$
上述方法得到的解 $x^*$ 在代理模型错误设定下，仍然具有较好的鲁棒性；同时最大最小( $\max \min$ )采集函数同样带来如下的问题：最大最小求得的解将趋向于保守(conservative)，很容易陷入局部最优解。
从贝叶斯优化框架的实现来看，我们面临如下的两个问题：

对于非凸、非凹的黑盒函数，很难找到全局的解；
贝叶斯优化框架中，代理函数和采集函数这两步是分开建模，并没有统一的计算框架让梯度在这两步间相互传播。

为解决上述问题，作者引入了带鲁棒性的采集函数：

$\max_{x} \alpha_{rob.}(\cdot) \equiv max_{x} \mathbb{E}_{\epsilon ~ N(0,\sigma_{\epsilon}^2 \mathbb{I})} [\alpha^{\theta + \epsilon }(x|D)] \tag{36}$
带鲁棒性的采集函数将尝试寻找能在一系列代理函数分布中，表现良好的候选点。带鲁棒性的采集函数实现，只需要获取代理函数(GPs)的均值和方差就可以实现。 如果 $\bar{\alpha}^{\theta} (x|D)= \alpha^{\theta} (x|D) + \eta \sigma_n , \eta \sim N(0,1)$ 成立，则对于任意的 $\rho \in (0,1)$ ,我们有：

上式说明，我们引入高斯噪音 $\epsilon \sim N(0,\sigma_\epsilon)^2 I$ ，能够使采集函数更加鲁棒。
6.3.3.2 多目标采集函数

我们前面提到，没有“一招鲜吃遍天”的方法。不同采集函数通常是冲突，经常会输出相反的候选点。针对这个问题，作者引入了多目标采集函数来获取帕累托最优解。多目标采集函数：

$\max(\alpha_{EI}^{\theta} (x|D) , \alpha_{PI}^{\theta} (x| D ) , \alpha_{UBC}^{\theta} (x|D) ) \tag{37}$

$\alpha_{Type}^{\theta} (x|D), Type \in \{ EI,PI, UCB \}$ , 为前面介绍的带鲁棒性的采集函数。关于多目标优化的知识，可以参考笔者的知乎专栏多目标优化总结综述。
求解多目标优化，通常有基于多目标梯度下降及进化算法。作者在这里使用了NSGA-II的进化算法来求解。
6.4 贝叶斯优化改进

处理异质方差性和不平稳性：

针对异质方差，对输出做转化(Transformation)

针对不平稳性，对输入做转化(Transformation)

共同提升

$\max(\alpha_{EI}^{\theta} (x|D) , \alpha_{PI}^{\theta} (x| D ) , \alpha_{UBC}^{\theta} (x|D) ) \\$
6.5 HEBO 核心代码解析

参考源代码：https://github.com/huawei-noah/HEBO/blob/master/HEBO/hebo/optimizers/hebo.py
主要由如下部分：

伪随机序列生成，具体可用参考笔者《超参数优化(三): 实验设计》部分
对X进行变换
对y进行变换
调用GPs模型，进行训练建模
GPs模型输出的最优候选点
构建采集函数
多目标采集函数优化
输出最优候选点

def suggest(self, n_suggestions=1, fix_input = None):
      if self.acq_cls != MACE and n_suggestions != 1:
         raise RuntimeError(&#39;Parallel optimization is supported only for MACE acquisition&#39;)
      if self.X.shape[0] < self.rand_sample:
         # 1. 伪随机序列生成，具体可用参考笔者《超参数优化(三): 实验设计》部分
         sample = self.quasi_sample(n_suggestions, fix_input)
         return sample
      else:
      # 2. 对X进行变换
         X, Xe = self.space.transform(self.X)
         try:
            # 3. 对y进行变换
            if self.y.min() <= 0:
                  y = torch.FloatTensor(power_transform(self.y / self.y.std(), method = &#39;yeo-johnson&#39;))
            else:
                  y = torch.FloatTensor(power_transform(self.y / self.y.std(), method = &#39;box-cox&#39;))
                  if y.std() < 0.5:
                     y = torch.FloatTensor(power_transform(self.y / self.y.std(), method = &#39;yeo-johnson&#39;))
            if y.std() < 0.5:
                  raise RuntimeError(&#39;Power transformation failed&#39;)
            # 4. 调用GPs模型，进行训练建模
            model = get_model(self.model_name, self.space.num_numeric, self.space.num_categorical, 1, **self.model_config)
            model.fit(X, Xe, y)
         except:
            y    = torch.FloatTensor(self.y).clone()
            model = get_model(self.model_name, self.space.num_numeric, self.space.num_categorical, 1, **self.model_config)
            model.fit(X, Xe, y)
         # 5. GPs模型输出的最优候选点
         best_id = self.get_best_id(fix_input)
         best_x  = self.X.iloc[[best_id]]
         best_y  = y.min()
         py_best, ps2_best = model.predict(*self.space.transform(best_x))
         py_best = py_best.detach().numpy().squeeze()
         ps_best = ps2_best.sqrt().detach().numpy().squeeze()

         iter  = max(1, self.X.shape[0] // n_suggestions)
         upsi  = 0.5
         delta = 0.01
         # kappa = np.sqrt(upsi * 2 * np.log(iter **  (2.0 + self.X.shape[1] / 2.0) * 3 * np.pi**2 / (3 * delta)))
         kappa = np.sqrt(upsi * 2 * ((2.0 + self.X.shape[1] / 2.0) * np.log(iter) + np.log(3 * np.pi**2 / (3 * delta))))
         # 6. 构建采集函数
         acq = self.acq_cls(model, best_y = py_best, kappa = kappa) # LCB < py_best
         mu  = Mean(model)
         sig = Sigma(model, linear_a = -1.)
         # 7. 多目标采集函数优化
         opt = EvolutionOpt(self.space, acq, pop = 100, iters = 100, verbose = False, es=self.es)
         rec = opt.optimize(initial_suggest = best_x, fix_input = fix_input).drop_duplicates()
         rec = rec[self.check_unique(rec)]
         # 8. 输出最优候选点
         cnt = 0
         while rec.shape[0] < n_suggestions:
            rand_rec = self.quasi_sample(n_suggestions - rec.shape[0], fix_input)
            rand_rec = rand_rec[self.check_unique(rand_rec)]
            rec    = rec.append(rand_rec, ignore_index = True)
            cnt +=  1
            if cnt > 3:
                  # sometimes the design space is so small that duplicated sampling is unavoidable
                  break
         if rec.shape[0] < n_suggestions:
            rand_rec = self.quasi_sample(n_suggestions - rec.shape[0], fix_input)
            rec    = rec.append(rand_rec, ignore_index = True)

         select_id = np.random.choice(rec.shape[0], n_suggestions, replace = False).tolist()
         x_guess = []
         with torch.no_grad():
            py_all    = mu(*self.space.transform(rec)).squeeze().numpy()
            ps_all    = -1 * sig(*self.space.transform(rec)).squeeze().numpy()
            best_pred_id = np.argmin(py_all)
            best_unce_id = np.argmax(ps_all)
            if best_unce_id not in select_id and n_suggestions > 2:
                  select_id[0]= best_unce_id
            if best_pred_id not in select_id and n_suggestions > 2:
                  select_id[1]= best_pred_id
            rec_selected = rec.iloc[select_id].copy()
         return rec_selected
6.6 总结

本文介绍的HEBO方法，在2020 BBO大赛和QQ浏览器2021AI算法大赛中表现都非常优异。HEBO算法框架仍然是贝叶斯优化（Bayesian Optimisation）。作者通过分析经典贝叶斯优化的数据输入、数据输出、代理模型和采集函数存在的问题和局限性，对每一步的问题都做了相应的优化：

对数据输入、数据输出进行变换校准；
将数据变换校准和GPs核函数联合在一起优化；
引入多目标采集函数，进行更鲁棒的探索（HEBO方法最大亮点)。

七、pySOT和POAP: 代理模型优化工具箱及其异步并行框架

摘要：POAP是一个以构建和组合多个异步优化策略，专门为解决黑盒函数全局优化问题而设计的事件驱动框架。pySOT是基于POAP框架，实现了同步和异步代理模型策略优化开源包。
本文主要内容参考[8] [9]：
7.1 简介

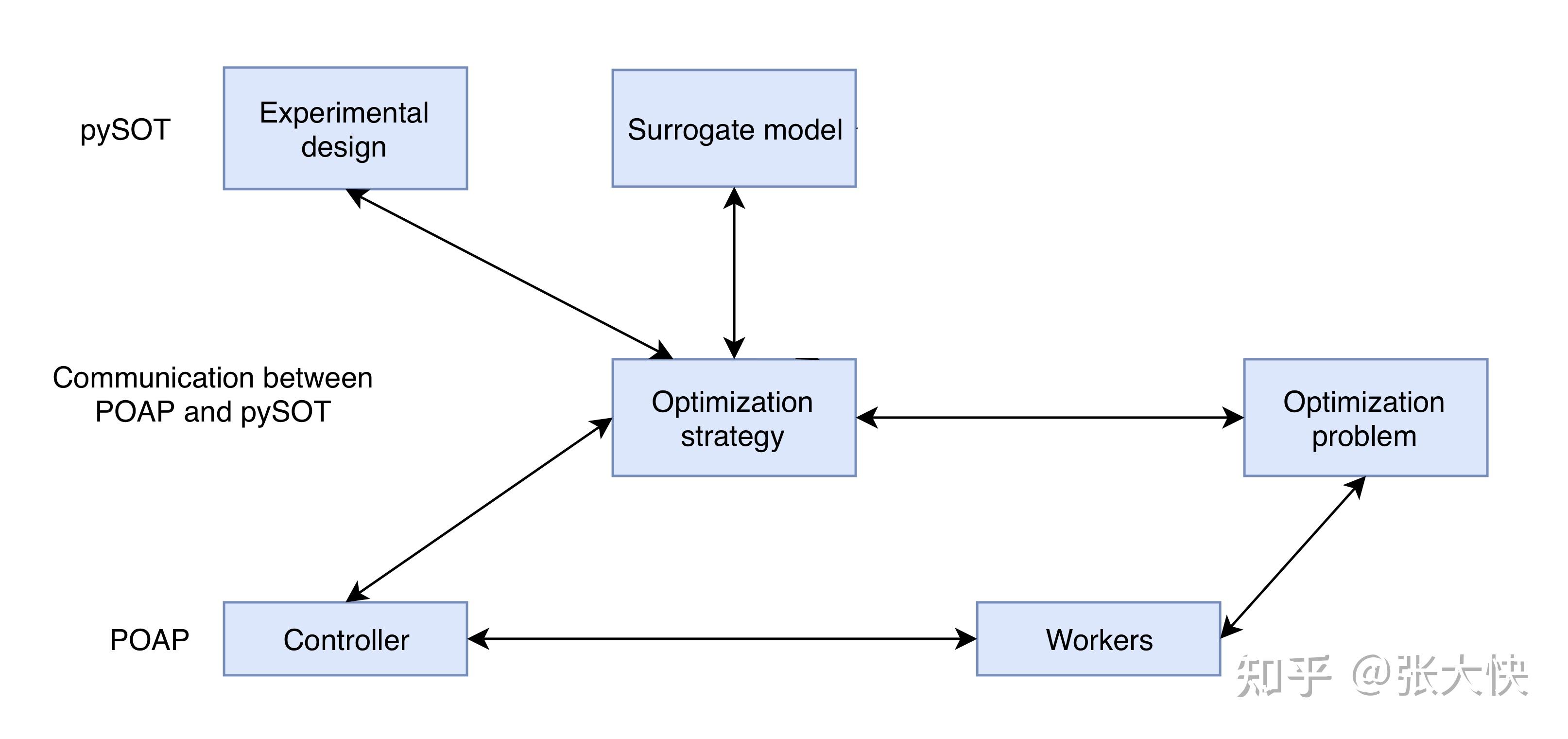
图7.1：pySOT和POAP整体框架

POAP是一个以构建和组合多个异步优化策略，专门为解决昂贵函数的全局优化问题而设计的事件驱动框架框架。POAP由三部分组成：

Worker Pool(从节点集合)：用于函数评估的求解；
Strategies(策略)：提议(propose)评估指令和其他动作到worker执行；
Controller(主控器)：处理和调节worker和strategies之间的通信。

pySOT是基于POAP框架，实现了同步和异步代理模型策略优化开源包。 pySOT和POAP框架，聚焦于求解如下的全局优化问题：

$\begin{aligned} \min_{x\in D} & f(x)\\ \text{s.t.} \enspace & x\in D \cap (\mathbb{Z}^q \times \mathbb{R}^{d-p}) \\ \end{aligned} \tag{38}$
其中 $f: \mathbb{Z}^q \times \mathbb{R}^{d-p} \rightarrow \mathbb{R}$ 是一个昂贵黑盒函数，同时假设是一个紧致的超立方（hypercube)，在内连续。 pySOT实现如下的模块:

策略和辅助问题：策略对象继承了POAP，支持候选点生成算法SRBF和DYCORS，以及采集函数EI和LCB；
实验设计：实现了拉丁超立方设计( Latin hypercube design,LHD )和对称拉丁超立方设计(symmetric Latin hypercube design,SLHD )；
代理模型：实现了径向基函数RBFs、GPs和MARS，多项式回归；
优化问题集合：实现了许多标准的测试评估集合，用来评估pySOT不同算法的性能。
检查点

7.2 代理模型优化

图7.2：同步代理函数优化算法

如上图所示，同不代理模型优化算法：

第1步：生成一个实验设计（通常有个点），；
第2步：评估在的值；
第3步：基于第2步的结果，构建的代理模型；
- 求解辅助问题（采集函数），选择下一个候选点
- 评估候选点函数值
- 更新代理模型

7.2.1 实验设计

实验设计概述可以参考本系列的第2章： https://zhuanlan.zhihu.com/p/433255266 最简单的实验设计是从超立方体中按 $2^d$ 个角(corners)采样，这种方法也叫2-factorial design 。在高维空间，这种方法是不可行的。另外两种可替代的方法是：

拉丁超立方设计( Latin hypercube design,LHD )
对称拉丁超立方设计(symmetric Latin hypercube design,SLHD )

7.2.2 代理模型：径向基函数

代理模型是用来近似目标函数（黑盒函数)。在pySOT中代理模型选取的是径向基函数(radial basis functions ,RBFs);同时也支持高斯过程回归(Gaussian processes , GPs)和支持向量回归(support vector regression , SVR)、多元逐步回归样条回归(multivariate adaptive regression splines , MARS)和多项式回归。

RBF插值函数

$g(x) = \sum_{i=1}^{N} w_i \phi(||x-x_i||) \tag{39}$

RBF 插值示意图[10]

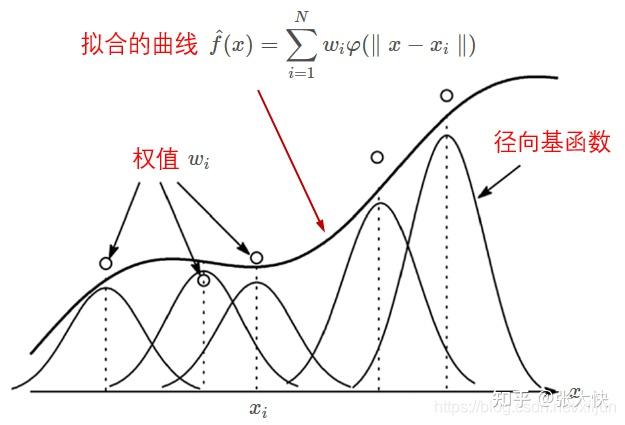
图7.3：径向基函数插值

图7.3：径向基函数插值
从上图可以看到，给定个已知的候选点集 $\{(x_i,f(x_i)| i=1...N \}$ 通过一系列的径向基函数，可以构造出相应的拟合函数曲线 $\hat{f}(x)$ 。
7.2.3 采集函数

可以参考本系列的第6章：6.2.2 采集函数假设 https://zhuanlan.zhihu.com/p/450107719
7.2.3.1 候选点生成

这里作者提出了一种平衡探索和利用(Exploration and Exploitation) 的新方法来生成候选点。主要的思想是生成一个候选点集合，使用评价函数（merit function)，从这个集合中挑选高潜力的候选点。对于每个 $x\in \Omega$ ，令 $\Delta(x)$ 为距离当前评估点集的距离。
定义如下公式来进行探索(Exploration):

$\begin{aligned} \Delta^{max} &= max\{ \Delta(x) : x \in \Omega \} \\ \Delta^{min} &= min\{ \Delta(x) : x \in \Omega \} \\ V^{D}(x) &= \frac{\Delta^{max} - \Delta(x) }{ \Delta^{max} - \Delta^{min}}\\ &其中0 \leq V^{D}(x) \leq 1 , \forall x\in \Omega \end{aligned} \tag{40}$

的值越小，说明当前的点是有效的探索。
定义如下公式来进行利用(Exploitation):

$\begin{aligned} s^{max} &= max \{ s(x) : x\in \Omega \}\\ s^{min} &= min \{ s(x) : x\in \Omega \}\\ V^{S}(x)&= \frac{s(x) - s^{min} } { s^{max} - s^{min} } \\ & 其中s(x)为代理模型\\ \end{aligned} \tag{41}$

的值越小，说明当前的点是有效的利用。
综合上面探索和利用的公式，最优候选点通过最小化如下的采集函数：

$\arg min_{x\in \Omega } merit(x) = w V^{S}(x) + (1+w) V^{D}(x)，w\in [0,1]\tag{42}$
候选点生成算法如下：

第1步：计算代理函数最大最小值: $s^{max} ,s^{min}$
第2步：计算利用值：
第3步：计算利用值：
第4步：生成候选点： $w V^{S}(x) + (1+w) V^{D}(x)$

图7.4：候选点生成算法

作者提出了两种策略：

LMS-RBF(SRBF Strategy) ，在处理低维问题比较有效。
DYCOR(DYCOR Strategy)，在处理高维问题比较有效。主要的思想是在优化初始阶段，对大部分的坐标进行扰动；在优化结束阶段对比少数坐标进行扰动。
这里通过对每个坐标维度进行扰动。给定个初始点，及最大评估次数 $N_{max}$ ,每一维坐标按如下的公式进行扰动： $p_{perturb}(n) = \min(\frac{20}{n},1) \times [1- \frac{log(n-n_{0})}{ log(N_{max} -n_0)}]\\ n_0 \leq n \leq N_{max} \\$

7.3 异步算法

前面提到的同步代理函数优化算法是比较容易实现的，但是不高效。作者基于事件驱动框架(POAP),实现了异步代理函数优化算法：

通过主控节点
驱动事件循环监听
更新代理模型
求解辅助问题。

图7.5：同步代理函数优化算法

图7.5：同步代理函数优化算法

第2-3行：初始参数和队列
第5-7行：将待评估候选点分发给从节点(worker)
第10-14行：如果评估成功，则更新 $X,f_{X}$ ；否则失败且需要重试，则重新放回评估队列
第16-122行：如果评估队列为空，则构建代理模型，求解辅助问题，将相应的候选点加入到队列中。下一步将评估点分发到从节点(worker)进行评估
第24行：返回最优候选点: $x_{best},f_{best}$

7.3.1 更新采样半径

在pySOT框架中，一个重要的问题是如何更新径向基函数的半径 $\sigma$ 。作者引入两个计数变量来实现更新：

，记录当前函数值成功的次数（这里指函数值相比前一个小的次数）， $C_{success} \leq F_{success}$ ；
,记录当前函数值失败的次数（这里指函数值相比前一个大的次数）， $C_{fail} \leq F_{fail}$ 。当迭代序列失败次数过多的时候，我们需要重启(restart)算法，避免陷入局部最优解。

图7.6：径向基函数半径调整算法

图7.6：径向基函数半径调整算法

第2-8行：当前点是有效点 :
- 记录当前最优值
- 计数加1， $C_{fail}=0$
第9-12行：当前点是五效点：
- 计数加1， $C_{success}=0$
第14-22行：如果成功次数或者失败次数达到上界
- 成功次数达到上界：将半径扩大2倍
- 失败次数达到上界：将半径缩小2倍
第24行：返回最优候选点

可以看到上面的径向基函数半径调整算法和前面的TuRBO算法的信赖域半径调整是类似的： https://zhuanlan.zhihu.com/p/436033362
7.6 代码示例

import logging
import os.path

import numpy as np
from poap.controller import BasicWorkerThread, ThreadController

from pySOT.experimental_design import SymmetricLatinHypercube
from pySOT.optimization_problems import Ackley
from pySOT.strategy import SRBFStrategy
from pySOT.surrogate import GPRegressor

def example_gp_regression():
if not os.path.exists(&#34;./logfiles&#34;):
      os.makedirs(&#34;logfiles&#34;)
if os.path.exists(&#34;./logfiles/example_gp.log&#34;):
      os.remove(&#34;./logfiles/example_gp.log&#34;)
logging.basicConfig(filename=&#34;./logfiles/example_gp.log&#34;, level=logging.INFO)

num_threads = 4
max_evals = 50
#测试函数
ackley = Ackley(dim=4)
# 高斯过程回归
gp = GPRegressor(dim=ackley.dim, lb=ackley.lb, ub=ackley.ub)
# 对称超拉丁方抽样
slhd = SymmetricLatinHypercube(dim=ackley.dim, num_pts=2 * (ackley.dim + 1))

# Create a strategy and a controller
# 创建controller
controller = ThreadController()
controller.strategy = SRBFStrategy(
      max_evals=max_evals, opt_prob=ackley, exp_design=slhd, surrogate=gp, asynchronous=True, batch_size=num_threads
)

print(&#34;Number of threads: {}&#34;.format(num_threads))
print(&#34;Maximum number of evaluations: {}&#34;.format(max_evals))
print(&#34;Strategy: {}&#34;.format(controller.strategy.__class__.__name__))
print(&#34;Experimental design: {}&#34;.format(slhd.__class__.__name__))
print(&#34;Surrogate: {}&#34;.format(gp.__class__.__name__))

# Launch the threads and give them access to the objective function
# 启动work
for _ in range(num_threads):
      worker = BasicWorkerThread(controller, ackley.eval)
      controller.launch_worker(worker)

# Run the optimization strategy
# 优化求解
result = controller.run()
# 输出结果
print(&#34;Best value found: {0}&#34;.format(result.value))
print(
      &#34;Best solution found: {0}\n&#34;.format(
         np.array_str(result.params[0], max_line_width=np.inf, precision=5, suppress_small=True)
      )
)

<hr/>欢迎关注: simplex101 ,了解更多超参数优化（黑盒优化）分享内容。
<hr/>参考文献

[1] QQ浏览器2021AI算法大赛，https://algo.browser.qq.com/
[2] Turner, Ryan, et al. &#34;Bayesian optimization is superior to random search for machine learning hyperparameter tuning: Analysis of the black-box optimization challenge 2020.&#34; arXiv preprint arXiv:2104.10201 (2021).
[3] TCowen-Rivers, Alexander I., et al. &#34;Hebo: Heteroscedastic evolutionary bayesian optimisation.&#34; arXiv e-prints (2020): arXiv-2012.
[4] Liu, Jiwei, Bojan Tunguz, and Gilberto Titericz. &#34;GPU Accelerated Exhaustive Search for Optimal Ensemble of Black-Box Optimization Algorithms.&#34; arXiv preprint arXiv:2012.04201 (2020).
[5] Sazanovich, Mikita, et al. &#34;Solving black-box optimization challenge via learning search space partition for local bayesian optimization.&#34; NeurIPS 2020 Competition and Demonstration Track. PMLR, 2021.
[6] Wang, Linnan, Rodrigo Fonseca, and Yuandong Tian. &#34;Learning search space partition for black-box optimization using monte carlo tree search.&#34; arXiv preprint arXiv:2007.00708 (2020).
[7] Eriksson, David, et al. &#34;Scalable global optimization via local bayesian optimization.&#34; Advances in Neural Information Processing Systems 32 (2019): 5496-5507.
[8] Eriksson, David, David Bindel, and Christine A. Shoemaker. &#34;pySOT and POAP: An event-driven asynchronous framework for surrogate optimization.&#34; arXiv preprint arXiv:1908.00420 (2019).
[9] Regis, Rommel G., and Christine A. Shoemaker. &#34;A stochastic radial basis function method for the global optimization of expensive functions.&#34; INFORMS Journal on Computing 19.4 (2007): 497-509.
[10] 基于径向基函数(RBF)的函数插值 ,基于径向基函数(RBF)的函数插值_zfoox的博客-CSDN博客_rbf插值
[11] 多目标优化总结：概念、算法和应用。知乎多目标优化专栏，https://www.zhihu.com/column/c_1360363335737843712
[12] 刘浩洋, 户将, 李勇锋，文再文，最优化：建模、算法与理论, 高教出版社，2020版
[13] Garud, Sushant S., Iftekhar A. Karimi, and Markus Kraft. &#34;Design of computer experiments: A review.&#34; Computers & Chemical Engineering 106 (2017): 71-95.
[14] Viana, Felipe AC. &#34;A tutorial on Latin hypercube design of experiments.&#34; Quality and reliability engineering international 32.5 (2016): 1975-1985.
[15] 崔佳旭, 杨博. 贝叶斯优化方法和应用综述[J]. 软件学报, 2018, 29(10): 3068-3090.
[16] Vu Nguyen. &#34;Tutorial on Recent Advances in Bayesian Optimization&#34; Asian Conference on Machine Learning (ACML), 2020.
[17] 江璞玉, 刘均, 周奇, 等. 大规模黑箱优化问题元启发式求解方法研究进展[J]. 中国舰船研究, 2021, 16(4): 1–18 doi: 10.19693/j.issn.1673-3185.02248
[18] Larson, Jeffrey, Matt Menickelly, and Stefan M. Wild. &#34;Derivative-free optimization methods.&#34; Acta Numerica 28 (2019): 287-404.
[19][朱尧辰（著）,《点集偏差引论》。中国科学技术大学出版社，2011.01]
[20] 康崇禄（著）,《蒙特卡罗方法理论和应用》。科学出版社，2015.
[21]试验设计。MBA百科。https://wiki.mbalib.com/wiki/DOE

		自动登录	找回密码
密码			立即注册

黑盒优化：超参数优化算法最新进展总结

本帖子中包含更多资源