论坛 › 技术讨论 Technology Answers › 排序算法中选择排序如何使用？

dollon 发表于 2024-7-15 17:47

排序算法中选择排序如何使用？

排序算法中选择排序如何使用？

dyanother 发表于 2024-7-15 17:47

在计算机科学中，排序算法是一种将数据元素按照某种顺序排列的算法。今天，我们要探讨的是选择排序（Selection Sort），这是一种简单直观的排序方法，通过不断选择剩余元素中的最小（或最大）元素，放到已排序序列的末尾，直到全部待排序的数据元素排完。
一、算法原理

选择排序的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。选择排序是不稳定的排序方法。
具体步骤如下：

[*]在未排序序列中找到最小（或最大）元素，存放到排序序列的起始位置。
[*]再从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。
[*]以此类推，直到所有元素均排序完毕。



在这里插入图片描述

二、代码实现

以下是使用Python语言实现选择排序的示例代码：
def selection_sort(arr):
    # 遍历所有数组元素
    for i in range(len(arr)):
      # 找到当前未排序部分的最小元素的下标
      min_idx = i
      for j in range(i+1, len(arr)):
            if arr < arr:
                min_idx = j
      # 将找到的最小元素和第一个未排序的元素交换位置
      arr, arr = arr, arr
    return arr

# 示例
arr =
print("原始数组：", arr)
sorted_arr = selection_sort(arr)
print("排序后的数组：", sorted_arr)三、算法分析

选择排序的时间复杂度为O(n^2)，其中n为待排序元素的数量。这是因为它包含两个嵌套的循环：外层循环遍历所有元素，内层循环用于查找当前未排序部分的最小元素。因此，尽管选择排序在某些情况下可能不是最高效的排序方法，但由于其实现简单且易于理解，它在教学和某些特定场景下仍然有其应用价值。
在空间复杂度方面，选择排序是原地排序，它只需要一个额外的空间来存储每次找到的最小元素的索引，因此其空间复杂度为O(1)。
四、优缺点

选择排序的优点是易于实现和理解，且不需要额外的存储空间（除了一个临时变量）。然而，它的缺点是时间效率较低，特别是在处理大规模数据时，其性能不如一些更先进的排序算法。
五、总结

选择排序是一种简单直观的排序方法，适用于小规模数据的排序。虽然它的时间效率不如某些更高级的排序算法，但在某些特定场景下，由于其实现简单和易于理解的特点，它仍然具有一定的应用价值。在实际应用中，我们需要根据具体的需求和数据特点来选择合适的排序算法。

wrj0619 发表于 2024-7-15 17:48

教程专栏持续更新中，关注不迷路~

攻略不讨喜的算法选择排序

选择排序每次把最小的元素拿出来，再把剩余元素中最小的元素拿出来，为了不使用额外空间，可以进行原地排序。

[*]从第一个元素开始对比，i 指向0，在剩余的元素中如果有比它更小的值位置 j 则换位置。
[*]接着遍历后面的数据，每次找到最小的值和当前的换位置。
array[0...i) 是有序的；array[i...n) 是无序的




简单实现

双层遍历， 每次寻找 i 后最小的一个元素， 和 i 处的元素换位置。
package org.example.sort;

// 选择排序法
public class SelectionSort {
    private SelectionSort(){}

    public static void sort(int[] arr) {
      for(int i = 0; i < arr.length; i++) {
            int minIndex = i;
            for(int j = i; j < arr.length; j++) {
                if(arr < arr)
                  minIndex = j;
            }
            swap(arr, i, minIndex);
      }
    }

    private static void swap(int[] arr, int i, int j){
      int t = arr;
      arr = arr;
      arr = t;
    }

    public static void main(String[] args) {
      Integer[] arrayNumber = { 2,8,5,9 };
      SelectionSort.sort(arrayNumber);
      Arrays.stream(arrayNumber).forEach(number -> System.out.print(number + " "));
    }
}

更通用的写法

加上泛型, E限制是Comparable 可比较的类型的数据.
public static <E extends Comparable<E>> void sortGeneric(E[] arr) {
      for(int i = 0; i < arr.length; i++) {
            int minIndex = i;
            for(int j = i; j < arr.length; j++) {
                if(arr.compareTo(arr) < 0)
                  minIndex = j;
            }
            swap(arr, i, minIndex);
      }
    }

public static void main(String[] args) {
      Integer[] arrayNumber = { 2,8,5,9 };
      SelectionSort.sortGeneric(arrayNumber);
      Arrays.stream(arrayNumber).forEach(number -> System.out.print(number + " "));
}

sexyrobto 发表于 2024-7-15 17:49

# 1.定义：
> 选择排序：一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

# 2.main
# 2.1 算法步骤
1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
3. 重复第二步，直到所有元素均排序完毕。
# 2.2 动图解析
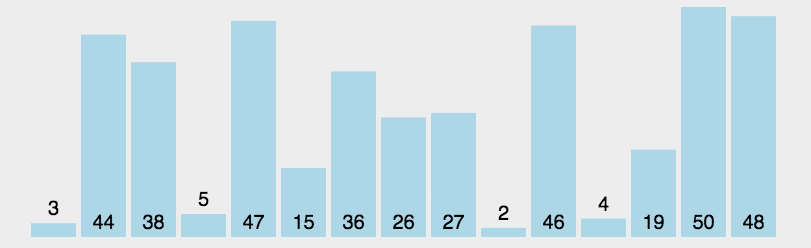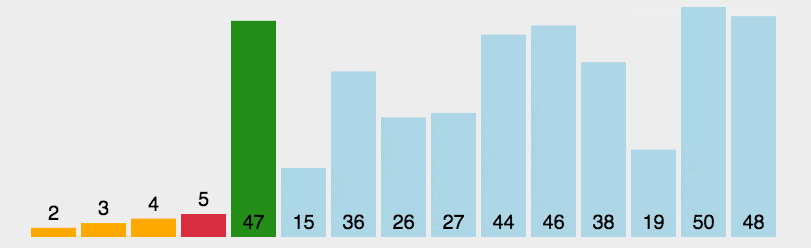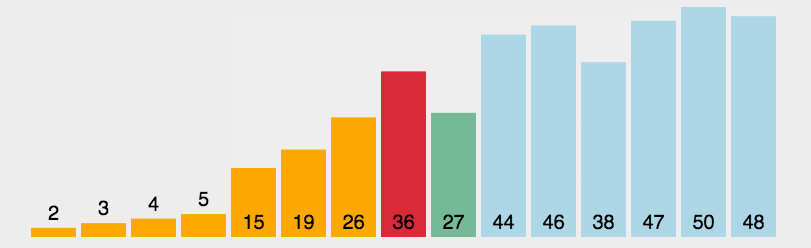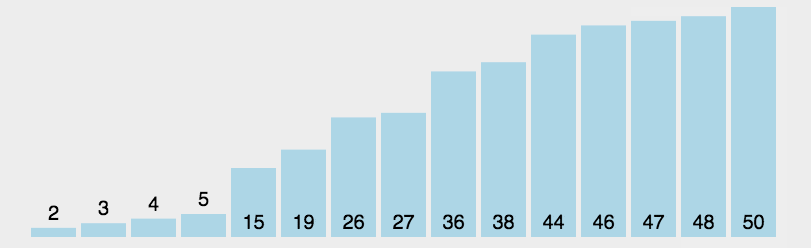
# 2.3 力扣做题分析
[力扣-颜色分类](力扣)
```javascript
/**
* @param {number[]} nums
* @return {void} Do not return anything, modify nums in-place instead.
*/
var sortColors = function(nums) {
    let n = nums.length
    for(let i = 0;i<n;i++){
      let min = i
      for(let j = i;j< n;j++){
            if(nums>nums) min = j
      }
      let tmp = nums
      nums = nums
      nums = tmp
    }
};
```
[力扣-判断能否形成等差数列](力扣)
```javascript
var SelectSort = function(nums) {
    let n = nums.length
    for(let i = 0;i<n;i++){
      let min = i
      for(let j = i;j< n;j++){
            if(nums>nums) min = j
      }
      let tmp = nums
      nums = nums
      nums = tmp
    }
};

var canMakeArithmeticProgression = function(arr) {
    SelectSort(arr)
    let d = arr - arr
    for(let i =0;i<arr.length - 1;i++){
      if(arr - arr !== d) return false
    }
    return true
};
```
[力扣-寻找序列的中位数](力扣)
```javascript
var SelectSort = function(nums) {
    let n = nums.length
    for(let i = 0;i<n;i++){
      let min = i
      for(let j = i;j< n;j++){
            if(nums>nums) min = j
      }
      let tmp = nums
      nums = nums
      nums = tmp
    }
};

var findMedianSortedArrays = function(nums1, nums2) {
   let nums = [...nums1, ...nums2]
   SelectSort(nums)
   const n = nums.length
   if (n % 2 === 0) return (nums + nums) / 2
   else return nums
};
```
[力扣- 至少是其他数字两倍的最大数](力扣)
```javascript
var SelectSort = function(nums) {
    let n = nums.length
    for(let i = 0;i<n;i++){
      let min = i
      for(let j = i;j< n;j++){
            if(nums>nums) min = j
      }
      let tmp = nums
      nums = nums
      nums = tmp
    }
};

var dominantIndex = function(nums) {
    let onums = [...nums]
    SelectSort(nums)
    let n = nums.length
    let max = nums
    let flag = 0
    for(let i=0;i<n - 1;i++){
      if(max < nums*2) flag = -1
    }
    return flag ? flag : onums.indexOf(max)
};
```
# 3.总结
选择排序是一种简单直观的排序算法。它通过重复从未排序的部分中选择最小的元素，并将其放到已经排序的部分的末尾，直到所有元素都排序完成。

选择排序的时间复杂度为O(n^2)，并且其稳定性较低，即相同元素的相对位置可能被打乱。由于其简单易懂的特点，选择排序通常用于小规模数据的排序任务，或作为其他排序算法的子过程。

总之，选择排序虽然不是最快的排序算法，但它易于理解和实现，在某些情况下仍然是一种比较合适的排序方法。当处理小规模数据时，选择排序可以在空间复杂度上有优势，因为它只需要一个额外的交换空间。

中国网站运营网 发表于 2024-7-15 17:49

思路


[*]每次选择第 i 小的数，并放到数组第 i 个位置
步骤


[*]初始化 i = 0 , 数组长度为 n
[*]在 nums 范围内寻找最小数的下标 p
[*]交换 nums 和 nums
[*]i 自增，跳转第二步直至 i=n-1
复杂度分析

第二步每次进行 n-1, n-2, ... 1 次比较：

https://www.zhihu.com/equation?tex=+%5Cfrac%7B1%7D%7B2%7Dn%28n+-+1+%2B+1%29+%3D+%5Cfrac%7Bn%5E2%7D%7B2%7D%5C%5C

交换需要进行 n 次，故选择排序时间复杂度为 O(n^2)
特点


[*]不同的输入不会影响排序的效率，即便是有序数组输入也需要O(n^2) 的复杂度
[*]交换次数为各个排序中最少的
实现

template<class T>
void selectionsort(T data [], int n) {
    for (int i = 0, j, least; i < n - 1; i++) {
      // Find the smallest item in , and put it in position i
      for (j = i + 1, least = i; j < n; ++j)
            if (data < data)
                least = j;
      std::swap(data, data);
    }
}

gaoyuhao 发表于 2024-7-15 17:50

配套源码地址：《八大排序》源码，提取码：5ehp哈喽，大家好，我是一条~



今天给大家带来《糊涂算法》专栏的第二期内容——排序算法的讲解。相信无论是初学者学习还是大厂面试，都少不了排序算法这关，即使没学过算法，对冒泡排序也不会陌生。
今天，一条就带大家彻底跨过「排序算法」这道坎，保姆级教程建议收藏。⭐️




准备

古语云：“兵马未动，粮草先行”。想跟着一条一块把「排序算法」弄明白的,建议先准备好以下代码模板。
观看本教程需知道基本循环语法、两数交换、双指针等前置知识。
建议先看完代码和逐步分析后再尝试自己写。

[*]新建一个Java工程,本文全篇也基于Java语言实现代码。
[*]建立如下目录结构





[*]在MainTest测试类中编写测试模板。
/**
* 测试类
* Author：一条
* Date：2021/09/23
*/
public class MainTest {
    public static void main(String[] args) {
      //待排序序列
      int[] array={6,10,4,5,2,8};
      //调用不同排序算法
      // BubbleSort.sort(array);
​
      // 创建有100000个随机数据的数组
      int[] costArray=new int;
      for (int i = 0; i < 100000; i++) {
            // 生成一个[0,100000) 的一个数
            costArray = (int) (Math.random() * 100000);
      }
​
      Date start = new Date();
      //过长，先注释掉逐步打印
      //BubbleSort.sort(costArray);
      Date end = new Date();
      System.out.println("耗时："+(end.getTime()-start.getTime())/1000+"s");
    }
}该段代码内容主要有两个功能：

[*]调用不同的排序算法进行测试
[*]测试不同排序算法将10w个数排好序需要的时间。更加具象的理解时间复杂度的不同

选择排序

基本思想

选择排序和冒泡排序很像，是从乱序序列的数据中，按指定的规则选出某一元素，再依规定交换位置后达到排序的目的。
动图讲解





代码实现

public class SelectSort {
    public static int[] sort(int[] array) {
      System.out.println("选择排序开始----------");
      for (int i = 0; i < array.length; i++) {
          //每个值只需与他后面的值进行比较，所以从开始
            for (int j = i; j < array.length; j++) {
            //注意此处是哪两个值比较
                if (array>array){
                  int temp=array;
                  array=array;
                  array=temp;
                }
            }
            System.out.println(Arrays.toString(array));
      }
      return array;
    }
}输出结果




逐步分析

[*]初始数组：
[*]拿出6与10比较，不交换 - > j++
[*]6与2比较，交换 - > j++
[*]注意此时是拿2继续比较，都不交换，确定第一位（最小的数）为2 - > i++
[*]循环下去，依次找到第一小，第二小，……的数
[*]最终结果 - >
这时再回去看动图理解。
耗时测试





时间复杂度：O(n^2)
算法优化

上诉代码中使用交换的方式找到较小值，还可以通过移动的方式，即全部比较完只交换一次。
这种对空间的占有率会有些增益，但对时间的增益几乎没有，可忽略，亦不再演示。
下一期：插入排序

查看完整版本: 排序算法中选择排序如何使用？